Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Prvočísla, kongruence, důkaz indukcí (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 10. 2015 13:50
Prvočísla, kongruence, důkaz indukcí
Dobrý den,
důkazy indukcí nebývají těžké a většinou se to dá nějak vymyslet. S tímto zadáním si nevím rady.
Nevím, jestli mi nechybí nějaká fajn věta, díky které to půjde snadno. Díky za jakoukoliv radu.
(to zadání má obecnější podobu, která se týká prvočísel, proto tento název tématu)
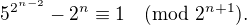
Prvních pár přirozených čísel:
n=1: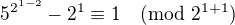
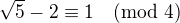
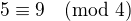
n=2:

ok
Vím-li tedy, že pro k přirozené číslo platí: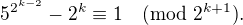
Jak z toho můžu ukázat, že platí i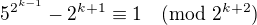
?
Mám to dělat úplnou indukcí, že bych předpokládal, že to platí pro k\inN a všechna čísla až do k?
Nejvíc mi asi vadí ten modul, podle kterýho se to dělá.
Ještě mě napadlo přepsat tu kongruenci podle nějaké ekvivalentní definice, třeba bych to v tom uviděl líp.
Zkusím pokračovat, kdyžtak dík za rady.
kolejo
Offline
- (téma jako vyřešené označil(a) kolejo)
#3 10. 10. 2015 15:23 — Editoval BakyX (10. 10. 2015 15:24)
Re: Prvočísla, kongruence, důkaz indukcí
Lemma:
Pre 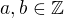 ,
,  platí:
platí: .
.
Dôkaz:
Riešenie:
1^6 - 2^6 + 3^6 = 666
Offline
#4 10. 10. 2015 15:50
Re: Prvočísla, kongruence, důkaz indukcí
↑ Rumburak:
↑ BakyX:
týjo, wow, díky, super
Nemám co dodat, asi, tak označím za vyřešené.
Zdravím, kolejo
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Prvočísla, kongruence, důkaz indukcí (TOTO TÉMA JE VYŘEŠENÉ)

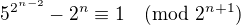 říká:
říká: takové, že
takové, že  .
.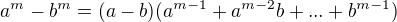
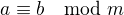 , takže
, takže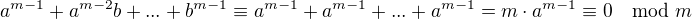 ,
,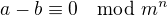 , takže dokopy
, takže dokopy  , čo sme chceli.
, čo sme chceli.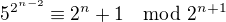
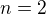 to platí. Nech to platí pre
to platí. Nech to platí pre 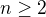 . Potom podľa lemmy:
. Potom podľa lemmy: