Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 10. 2015 13:13
Indukce
Dobrý den,
objevil jsem celkem značné mezery, které teď na sebe nechávají znát víc než kdy jindy.
Mám problém s tímto příkladem na mat. indukci a ať tam hledám sebevíc, stále nic nenacházím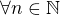 platí
platí
Pro n = 1 to platí
Pokud předpokládáme, že to platí pro n=k, potom to platí i pro n=k+1
Jenže zde vůbec netuším, jak tam najít ten indukční předpoklad, jelikož v závorce na RHS je (k+2)/2 a ne (k+1)/2
Děkuji.
Freedy
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 11. 10. 2015 15:39 — Editoval Freedy (11. 10. 2015 15:43)
Re: Indukce
No tak upravit P(n) ale jak?
potom:

zde mě napadá ještě úprava na:
Nebo tohle je úplně špatná cesta???
Já už se v tom asi začínám úplně ztrácet.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#7 11. 10. 2015 15:46
Re: Indukce
Já tam odhady právě že žádné nepletu.
Jen se nějak (asi marně) snažím upravit člen P(n).
Vždyť přece, jestli má platit: a indukční předpoklad je:
a indukční předpoklad je: tak z toho plyne, že musí platit:
tak z toho plyne, že musí platit: ne?
ne?
A to sem se právě snažil dokázat...
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#10 11. 10. 2015 16:03
Re: Indukce
Ahoj
Pozri aj sem
http://forum.matweb.cz/viewtopic.php?id=86167
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 11. 10. 2015 16:18
Re: Indukce
Ano,
takže v podstatě a jelikož je e/2 větší než jedna, tak potom je logické, že:
a jelikož je e/2 větší než jedna, tak potom je logické, že:
↑ Bati: díky moc, jenom dotaz, proč jsi tam přidal to epsilon? Aby jsi se dostal k tomu přesnému výrazu (n+1)! ?
Díky
Freedy
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#16 13. 10. 2015 13:35
Re: Indukce
To je pravda
 což je ekvivalentní s posledním výrokem:
což je ekvivalentní s posledním výrokem: a toto lze dokázat (například pomocí bernoulliho nerovnosti), případně indukcí.
a toto lze dokázat (například pomocí bernoulliho nerovnosti), případně indukcí.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline


 ,
, .
.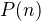 .
.
 . Teď použiješ rovnost, kterou jsem psal:
. Teď použiješ rovnost, kterou jsem psal: .
.
 a tím pádem to bude stále "víc"
a tím pádem to bude stále "víc"



