Matematické Fórum

malarad · 15. 10. 2015 03:17

Dobré ráno moji milí, prosím o nápovědu k paní limitce a odůvodnění proč to tak mám začít počítat. Zkoušel jsem čitatele i jmenovatele vydělit $x$ , ale nevím s jakou mocninou výraz děliti.
$\lim_{x\to\infty }\frac{x+1}{\sqrt{x-1}+2}$

Al1 · 15. 10. 2015 07:13 — Editoval Al1 (15. 10. 2015 07:14)

↑ malarad:

Zdravím,

já v tomto případě užiji vytýkání
$\lim_{x\to\infty }\frac{x\bigg(1+\frac{1}{x}\bigg)}{\sqrt{x}\bigg(\sqrt{1-\frac{1}{x}}+\frac{2}{\sqrt{x}}\bigg)}$

a teď pokrátím

malarad · 15. 10. 2015 12:31

↑ Al1:
Díky, je to takhle? Tři členy jdou k nule, vyšlo mi to jako nekonečno lomeno odmocnina z nekonečna. Pokud je to dobře...Pokud ano, tak nevím jesti se oba rovnají, nebo jestli je odmocnina z nekonečna menší než nekonečno, protože jsem četl, že odmocnina z nekonečna je zase nekonečno.
//forum.matweb.cz/upload3/img/2015-10/04583_5858.JPG

Jj · 15. 10. 2015 12:40

↑ malarad:

Dobrý den. Řekl bych, postupovat podle rady kolegy ↑ Al1:, tzn. nejdříve krátit:

$\frac{x}{\sqrt{x}}=\frac{x\sqrt{x}}{x}=\frac{\sqrt{x}}{1}$

malarad · 15. 10. 2015 12:55

↑ Jj:
Děkuju, takže ten můj výsledek $\frac{\infty }{\sqrt{\infty }}$ není špatně? ale je těžko URČITELNÝ, po zkrácení je to už "vidět", že výsledek je nekonečo.
ještě se chci zeptat, jestli odmocnina z nekonečna je opravdu nekonečno?, já se domnívám že ano.

Formol · 15. 10. 2015 12:59 — Editoval Formol (15. 10. 2015 13:22)

↑ malarad:
Dovolím si odpovědět za kolegu. Obecně platí:
$\lim_{x\rightarrow\infty} f(x) = \infty$

pro každou funkci, která je od nějakého x0 rostoucí. Na tomhle poznatku stojí většina "uhádnutí" dílčích limit.

Edit: Samozřejmě to platí jen pro rostoucí shora neomezenou funkci...

malarad · 15. 10. 2015 13:12

↑ Formol:
díky, takže z definice, kterou jsi uvedl vyplývá, že odmocnina z nekonečna je zase nekonečno.

což však znamená, že $\frac{\infty }{\sqrt{\infty }}$ = $\frac{\infty }{\infty }$ ??? ale to by znamenalo výsledek $1$ ? Když mám něco děleno tím samým...

Bati · 15. 10. 2015 13:16 — Editoval Bati (15. 10. 2015 13:21)

Ahoj ↑ malarad:
$\sqrt{\infty}$ se nedefinuje, protože to není potřeba (u limit). Důvod, proč ti takové nesmysly vychází je to, že nepíšeš limitu tam, kde by měla být - viz tvůj výpočet:
$\lim_{x\to\infty}\frac{x}{\sqrt{x}}=\infty$ , ale $\frac{\infty}{\sqrt\infty}$ je obrázek bez významu.

Pokud si zakážeš dělat jakékoliv matematické operace s nekonečnem, uděláš jedině dobře.

Formol · 15. 10. 2015 13:18 — Editoval Formol (15. 10. 2015 13:19)

↑ malarad:
Hodnota 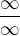$\frac{\infty }{\infty }$ není (v matematické analýze) nijak definována. Proto musíš výraz upravit tak, aby měl jiný tvar, nebo se zamyslet nad tím, zda jsou splněny podmínky pro použití L'Hospitalova pravidla. L'Hospital je zde kanón na vrabce, ale můžeš udělat to, co kolega Jj výše doporučil:
$\frac{x}{\sqrt{x}}=\frac{\sqrt{x}\sqrt{x}}{\sqrt{x}}=\frac{\sqrt{x}}{1}=\sqrt{x},\;\;x>0$

A takový výraz, když poženeš limitou k nekonečnu, už povede k něčemu, co je definované.

Rumburak · 15. 10. 2015 13:30

↑ malarad:

Ahoj.

Další možnost je přes substituci $\sqrt{x-1} = y$ , tj. $x = y^2 + 1$ , při čemž platí

$\lim_{x\to\infty}\frac{x+1}{\sqrt{x-1}+2} = \lim_{y\to\infty}\frac{ y^2 + 2}{y+2}$

a lze nyní použít standardní postup pro limitu podílu polynomů (v nevlastním bodě).

Viz též věta o limitě složené funkce, na níž je substituce v limitě založena.

malarad · 15. 10. 2015 13:31

moc děkuju všem za odpovědi

Matematické Fórum

#1 15. 10. 2015 03:17

limitka

#2 15. 10. 2015 07:13 — Editoval Al1 (15. 10. 2015 07:14)

Re: limitka

#3 15. 10. 2015 12:31

Re: limitka

#4 15. 10. 2015 12:40

Re: limitka

#5 15. 10. 2015 12:55

Re: limitka

#6 15. 10. 2015 12:59 — Editoval Formol (15. 10. 2015 13:22)

Re: limitka

#7 15. 10. 2015 13:12

Re: limitka

#8 15. 10. 2015 13:16 — Editoval Bati (15. 10. 2015 13:21)

Re: limitka

#9 15. 10. 2015 13:18 — Editoval Formol (15. 10. 2015 13:19)

Re: limitka

#10 15. 10. 2015 13:30

Re: limitka

#11 15. 10. 2015 13:31

Re: limitka

Zápatí