Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz existence suprema shora omezene posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
#2 06. 02. 2009 14:13 — Editoval lukaszh (06. 02. 2009 14:14)
Re: Důkaz existence suprema shora omezene posloupnosti
Keď je postupnosť  zhora obmedzená tak existuje
zhora obmedzená tak existuje  , že pre všetky
, že pre všetky  . No a to je vlastnosť supréma. Ešte treba dokázať existenciu prvku
. No a to je vlastnosť supréma. Ešte treba dokázať existenciu prvku  takého, že
takého, že  , čo je zrejmé.
, čo je zrejmé.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#3 06. 02. 2009 14:25 — Editoval Ginco (06. 02. 2009 14:25)
Re: Důkaz existence suprema shora omezene posloupnosti
↑ lukaszh: ok dík...zdá se to být korektní důkaz
ješte dotaz : Jaký je vztah mezi :  ...
... 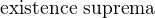 ....
.... 
myslim, ze se kazda implikuje s kazdou, ale je terba to nejak objasnit....vím co kazda znamena, ted uz bych udelal ke kazdemu principu i dukaz, ale ...
Offline
#4 06. 02. 2009 14:51
Re: Důkaz existence suprema shora omezene posloupnosti
↑ lukaszh:
Řekl bych, že korektní důkaz vyžaduje mnohem detailnější úvahy. Stačí si prostudovat důkaz v Diferenciálním počtu I od Jarníka. Podobně na tom je i důkaz v knize Reálne čísla od Tibora Šaláta.
Offline
#5 06. 02. 2009 14:52
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Důkaz existence suprema shora omezene posloupnosti
↑ lukaszh:
Já ten důkaz nevidím tak jednoduše. Posloupnost 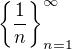 je omezená např.
je omezená např.  . To ale jistě není supremum.
. To ale jistě není supremum.
Offline
#6 06. 02. 2009 14:53 — Editoval Marian (06. 02. 2009 14:54)
Re: Důkaz existence suprema shora omezene posloupnosti
↑ BrozekP:
To jsem si také říkal, ale lukaszh neříká, že je to vlastnost jediná. Jinak je to neúplné a velmi nepřesné - musím souhlasit.
Offline
#7 06. 02. 2009 14:55
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Důkaz existence suprema shora omezene posloupnosti
↑ Marian:
Lukaszh dále uvažuje jako kdyby chtěl ukázat, že  je supremum, proto ta reakce.
je supremum, proto ta reakce.
Offline
#8 06. 02. 2009 14:57
#9 06. 02. 2009 15:08
Re: Důkaz existence suprema shora omezene posloupnosti
↑ Marian:
mam ten důkaz v knize MA1 Drábek Míka...řeší se přes princip vložených intervalů...ok beru tedy zpět, že důkaz je korektni, ale čím je důkaz jednodušši, tím je pro mě přijatelnejsi :-D , ovšem krása důkazu je v jehokorektnosti :-) jinak mohli byste mi poradit s otazkou no. 2 ? děkuji
Offline
#10 06. 02. 2009 16:03
Re: Důkaz existence suprema shora omezene posloupnosti
↑ Marian: ↑ BrozekP:
Ja som to skôr myslel tak, že ešte pre ľubovoľne malé epsilon platí uvedená nerovnosť. Tým by sa ukázala druhá vlastnosť supréma. Nevidím na tom nič podradné.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#11 06. 02. 2009 16:26
Re: Důkaz existence suprema shora omezene posloupnosti
↑ Ginco:
Nevím přesně co je Axiom úplnosti, ale v důkazu principu vložených intervalů se používá věta, že shora omezená rostoucí posloupnost má vlastní limitu a v důkaze této věty se zase používá věta, že omezená posloupnost má supremum ... jinak nějaký magický vztah bych tam asi nehledal.
Offline
#12 18. 02. 2009 11:35 — Editoval Rumburak (18. 02. 2009 16:00)
Re: Důkaz existence suprema shora omezene posloupnosti
Supremum posloupnosti je definováno jako supremum množiny hodnot této posloupnosti, existence suprema posloupnosti je tím převedena
na existenci suprema množiny. Existenci suprema shora omezené množiny lze dokázat na základě příslušné konstrukce množiny reálných čísel
z čísel racionálních. Z nejznámějších konstrukcí je to Dedekindova teorie řezů (viz V.Jarník: Diferenciální počet I. ) nebo Cantorova metoda zúplnění
metrického prostoru (viz - domnívám se - E.Čech: Bodové množiny). Důkazy v obou těchto teoriích se přirozeně liší.
Ve školské matematice bývá (pro zjednodušení) teorie reálných čísel axiomatizována: reálná čísla tvoří uspořádané komutativní těleso, v němž platí
"cosi navíc", než v tělese čísel racionálních. To "cosi navíc" může být vyjádřeno buďto axiomem o supremu
(S) "každá neprázdná shora omezená množina reálných čísel má v množině reálných čísel supremum"
nebo axiomem úplnosti
(U) "každá posloupnost reálných čísel splňující Bolzano-Cauchyovu podmínku (jinými slovy cauchyovská posloupnost) má v množině reálných čísel limitu"
(což v topologické terminologii znamená, že prostor reálných čísel je úplný). Obě tato tvrzení (S) a (U) jsou pak ekvivalentní, tj. přijmeme-li jedno
z nich jako axiom, pak to druhé lze dokázat jako větu.
Metoda vložených intervalů je patrně tvrzení Cantorovy věty
(C) "Jsou-li { a_n }, { b_n } posloupnosti reálných čísel (n je index) splňující nerovnost a_n <= a_n+1 < b_n+1 <= b_n ,
potom průnik všech uzavřených intervalů [ a_n , b_n ] (míněny intervaly v množině reálných čísel) při n = 1, 2, ... je neprázdný. "
Tvrzení (C) je jedním z dalších ekvinalentů k (S) resp. (U).
Offline
#13 20. 10. 2015 20:07
Re: Důkaz existence suprema shora omezene posloupnosti
↑ Rumburak:
Zdravím, nevíte o nějakém materiálu, kde by byly důkazy vzájemné ekvivalence mezi (S), (U), (C), axiomem infima a axiomem spojitosti? Díky.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#14 21. 10. 2015 12:26
Re: Důkaz existence suprema shora omezene posloupnosti
↑ byk7:
Zdravím.
Něco z toho by se jistě dalo nalézt v Diferenciálním počtu 1 resp. 2 od Vojtěcha Jarníka,
kde jsou i seznamy další literatury.
Samotné důkazy nejsou nijak zvlášť obtížné, pokud máme zvládnuty defiinice příslušných pojmů
a zažíty běžné důkazové technky ze základů analýzy. Případně zde můžeme něco z toho probrat,
i když můj přístup k internetu není poslední dobou pravidelný.
Offline
#15 23. 10. 2015 11:54 — Editoval Rumburak (23. 10. 2015 13:00)
Re: Důkaz existence suprema shora omezene posloupnosti
Svůj předchozí příspěvek ještě poněkud doplním.
Především je potřeba uvědomit si toto:
V tělese reálných čísel platí ekvivalence  , pomocí níž lze zřejmým způsobem
, pomocí níž lze zřejmým způsobem
- nejmenší prvek množiny  vyjádřit pomocí největšího prvku množiny
vyjádřit pomocí největšího prvku množiny 
a naopak,
- horní závoru množiny  vyjádřit pomocí dolní závory množiny
vyjádřit pomocí dolní závory množiny  a naopak,
a naopak,
- vlastnosti nerostoucí posloupnosti  odvodit z vlastností neklesající posloupnosti
odvodit z vlastností neklesající posloupnosti  a naopak,
a naopak,
a podobně. Tyto analogie se často využívají a v následujícím textu už na ně (v zájmu přehlednosti) nechci
odkazovat.
Hledaný důkaz, že jistá tvrzení o reálných číslech jsou ekvivalentní s větou o supremu, by mohl mít následující
cyklickou strukturu :
I. Pomocí předpokladu, že každá neprázdná shora omezená podmnožina množiny  (všech reálných čísel)
(všech reálných čísel)
má supremum v  , lze dokázat, že každá neklesajíci shora omezená poslpoupnost
, lze dokázat, že každá neklesajíci shora omezená poslpoupnost  má limitu v
má limitu v 
a touto limitou je supremum množiny všech hodnot uvažované posloupnosti.
II. Z předchozího výsledku lze odvodit Cantorovu větu o neprázdném průniku posloupnosti uzavřených
intervalů  splňujících podmínku
splňujících podmínku  pro všechny hodnoty indexu
pro všechny hodnoty indexu  .
.
III. Z posledního výsledku lze odvodit, že z každé omezené posloupnosti reálných čísel lze vybrat
posloupnost konvergentní.
IV. Odtud lze dokázat, že
(*) každá posloupnost reálných čísel splňující B-C podmínku má limitu v  .
.
V. Předpokládáme-li místo věty o supremu, že platí tvrzení (*) , potom lze větu o supremu dokázat tak, že
k dané neprázdné shora omezené množině  sestrojíme vhodnou posloupnost (spňuijící B-C podmínku),
sestrojíme vhodnou posloupnost (spňuijící B-C podmínku),
o jejíž limitě pak ukážeme, že je zároveň nejmenší horní závorou množiny  .
.
Ještě k axiomu spojitost:
Je-li podmnožina  množiny
množiny  neprázdná a shora omezená, pak jsou neprázdné i množiny
neprázdná a shora omezená, pak jsou neprázdné i množiny  - množina všech horních závor množiny
- množina všech horních závor množiny  v
v  ,
, 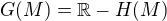 .
.
Zřejme platí  . Podle axiomu spojitosti pak existuje reálné
. Podle axiomu spojitosti pak existuje reálné  ,
,
které je horní závorou množiny  a zároveň dolní závorou množiny
a zároveň dolní závorou množiny  . Snadno nahlédneme, že jde
. Snadno nahlédneme, že jde
o nejmenší horní závoru množiny  . Tím by byla dokázana věta o supremu na základě ax. spojitosti.
. Tím by byla dokázana věta o supremu na základě ax. spojitosti.
Důkaz opačným směrem také není těžký.
Offline
#16 26. 10. 2015 21:21
Re: Důkaz existence suprema shora omezene posloupnosti
↑ Rumburak:
Díky, dneska jsem si všiml, že ve skriptech je dodatek věnovaný právě tvrzením, která jsou ekvivalentní axiomu suprema. Projdu si to, a když mi bide něco nejasného, dám vědět. :-)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz existence suprema shora omezene posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
