Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 10. 2015 15:41
důkaz supremum f(x) g(x)
Dobrý den,
rád bych se zeptal na správnou formulaci při dokazování tohoto tvrzení a i menší pomoc.
Mám najít vztah, mezi dvěma omezenými (spojitost není podmínkou) funkcemi (z R do R) (stejné x)
(stejné x) 
Nemám problém s tím, když funkce f a g budou "podobné" v tom smyslu, že k supremu se budou blížit na stejném, libovolně malém intervalu. Pak by totiž šlo psát:

Sečtením posledních dvou nerovností dostávám: . Platí tedy, že
. Platí tedy, že  pro nabývání suprema na libovolně malém stejném intervalu.
pro nabývání suprema na libovolně malém stejném intervalu.
Nicméně, jak nyní ukážu, že ten vztah má být "menší rovno" ?
Kdybych měl funkce třeba arctan(x) a -(arctan(x))?
Mohl bych to třeba ukázat sporem tak, že bych předpokládal, že se to rovná vždy a pak bych uvedl příklad třeba s těmi arkus tangensy?
Děkuji za nápovědu.
Freedy
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#3 31. 10. 2015 22:21
Re: důkaz supremum f(x) g(x)
↑ Bati:
ahoj,
děkuji... Hned to vypadá snáz. Nenapadlo mě zvolit pevné x (což nechápu proč)
Tyhle techniky se mi budou určitě budou hodit u dalších příkladů. Zatím mi důkazové úlohy vůbec nejdou ://.
Jinak ano, funkce jsou ze zadání omezené.
Mám takovou podotázku ještě. Jak jsi v závěru zmínil neomezenost, tak potom by tam ten symbol nešel dát ne?
Chápu, že pro normální funkce by muselo stále platit  protože shora neomezená funkce by měla poté supremum +nekonečno. Nicméně, co kdybych měl dvě funkce:
protože shora neomezená funkce by měla poté supremum +nekonečno. Nicméně, co kdybych měl dvě funkce: zde je
zde je 
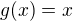 zde je
zde je  takže výraz na pravé straně není definován.
takže výraz na pravé straně není definován.
Popřípadě jak jsi myslel, že nemusíme předpokládat nic? -.-
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 31. 10. 2015 22:41
Re: důkaz supremum f(x) g(x)
Aha... Zkoušel jsem jen nějak napasovat f(x) na prázdnou množinu. Šlo by to tedy nějak jinak?
Mimochodem, proč to není reálná funkce. Zkrátka 
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#6 31. 10. 2015 23:24
Re: důkaz supremum f(x) g(x)
↑ Freedy:
Pokud děláš suprema přes R, pak by tam ty funkce měly bejt taky definovaný ne? A pokud bys chtěl opravdu uvažovat takový nesmysly jako prázdný definiční obory, tak si tam můžeš přidat předpoklad, že pravá strana musí existovat, což není jinak vůbec omezující.
A k tomu důkazu..psal jsi, že volím pevné x, což není úplně pravda. Samotné x probíhá R, ale předpokládám, že jsi myslel x0. To je sice pevné, ale nevolím ho, protože nějak závisí na epsilon, které volím.
Offline
#7 31. 10. 2015 23:28
Re: důkaz supremum f(x) g(x)
Ano, špatně jsem se vyjádřil. Bral jsi, že existuje takové x, že je větší než supremum - epsilon, pro libovolně malé epsilon. A pak jsi ukázal, že f(x0) + g(x0) musí být nutně menší rovno než sup f(x) + sup g(x).
Tohle je v pořádku.
A vymýšlet nesmysly opravdu nemám zapotřebí. Jen jsem chtěl zkontrolovat jedinou možnost v R*, kdy by výraz napravo nebyl definován.
Freedy
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#9 31. 10. 2015 23:46
Re: důkaz supremum f(x) g(x)
↑ Bati:
to je pravda. To vychází z definice suprema. 
 sečtením pak
sečtením pak a teď už stačí položit x1 = x2 = x0.
a teď už stačí položit x1 = x2 = x0.
Teď se normálně za svoji původní otázku stydím -.- Asi se příště radši víc zamyslím.
Jinak dobrý postřeh s tím R*. Toto mě nenapadlo.
Nicméně opravdu nenajdu reálnou funkci, která by měla obor hodnot prázdnou množinu? (proč?)
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#11 01. 11. 2015 00:07
Re: důkaz supremum f(x) g(x)
Mně náhodou přijde zajímavé u prázdné množiny to, že je to v podstatě jediná množina, kde platí:
Mimochodem, jak by to vypadalo se supremem u tý funkce, jak jsi psal v R*  . Bylo by to rovněž
. Bylo by to rovněž  stejně jako infimum?
stejně jako infimum?
A nepřijde mi, že prázdné množiny jsou k ničemu. Je to speciální případ. Který se "většinou" musí vyšetřovat zvlášť.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline

 .
. .
. je omezená, ale pokud není, pak je to triviální, tzn., že nemusíš předpokládat nic.
je omezená, ale pokud není, pak je to triviální, tzn., že nemusíš předpokládat nic. .
.