Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » veta o dlhom a širokom (TOTO TÉMA JE VYŘEŠENÉ)
#1 02. 11. 2015 19:54
veta o dlhom a širokom
zdravím
vedel by mi niekto pomôcť, ako dokázať nasledujúce tvrdenie ?
Dokažte, že věta O Dlouhém a Širokém je nejlepší možná v následujícím smyslu:  existuje čiastočne usporiadaná množina
existuje čiastočne usporiadaná množina  s
s  prvky splňující
prvky splňující  ,
, 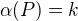 a
a  (Tzn. nalezněte takovou částočně uspořádanou množinu pre libovolné
(Tzn. nalezněte takovou částočně uspořádanou množinu pre libovolné  )
)
veta o dlhom a širokom: Nech  je čiastočne usporiadaná množina,
je čiastočne usporiadaná množina,  je najdlhší antireťazec v P a
je najdlhší antireťazec v P a  je najdlhší reťazec v P, potom
je najdlhší reťazec v P, potom 
ďakujem za každú radu.
Per aspera ad astra
Offline
- (téma jako vyřešené označil(a) byk7)
#2 02. 11. 2015 20:28
Re: veta o dlhom a širokom
↑ vytautas:
Ahoj.
Nevím, jestli to není úplně mimo, ale co takhle k nezávislých řetězců délky l ?
What does a drowning number theorist say?
'log log log log ...'
Offline
#3 02. 11. 2015 20:53 — Editoval vytautas (02. 11. 2015 20:59)
Re: veta o dlhom a širokom
hmm, to znie rozumne. Nejaký nápad ako to formálnejšie dokázať ? ďakujem
edit. neviem, ako mám chápať niečo ako "nezávislý reťazec". Mám nezávislú množinu (antireťazec/antichain) a reťazce (chain).
Ak by som si zobral  antireťazcov s dĺžkou
antireťazcov s dĺžkou  a "vybudoval" z nich množinu, stále nemám zaručené, že tam bude existovať reťazec dĺžky
a "vybudoval" z nich množinu, stále nemám zaručené, že tam bude existovať reťazec dĺžky  , či ?
, či ?
Per aspera ad astra
Offline
#5 02. 11. 2015 21:14
Re: veta o dlhom a širokom
↑ Andrejka3:
aha, jasné, teraz to už vidím . čo sa týka formálnosti dôkazu ? :) nejaký hint ?
Per aspera ad astra
Offline
#6 02. 11. 2015 21:44
Re: veta o dlhom a širokom
↑ vytautas:
Jak moc formální? Dívej, co se mi stane, když chci být formálnější:
Máme množinu  , kde
, kde 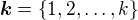 .
.
Uspořádání  , kde T je tranzitivní uzávěr. Teď příklad maximálního řetězce a že má každý stejně prvků a max antiř a že má každý stejně prvků.
, kde T je tranzitivní uzávěr. Teď příklad maximálního řetězce a že má každý stejně prvků a max antiř a že má každý stejně prvků.
Prostě to vypadá hrozně, přitom obrázek je jasný.
To si už napíšeš sám...
What does a drowning number theorist say?
'log log log log ...'
Offline
#7 02. 11. 2015 21:56
Re: veta o dlhom a širokom
↑ Andrejka3:
už som to ako tak spísal.
ďakujem krásne, za ochotu hlavne, veľmi mi to pomohlo :)
Per aspera ad astra
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » veta o dlhom a širokom (TOTO TÉMA JE VYŘEŠENÉ)
