Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 11. 2015 19:40
Operace s přirozenými čísly
Ahojte,
nevím kam to zařadit, tak jsem to dal sem. Měl bych dotaz na toto:
Hledám taková přirozená čísla a,b, pro která platí, že výsledkem následující operace s nimi je opět přirozené číslo n
Postupným zkoušením jsem takovou dvojici čísel našel, ale zajímalo by mě, jestli existuje nějaký návod, pomůcka jak ji najít, či důkaz toho, že taková dvojice pro daný vztah (i jiný) neexistuje.
Díky
Offline
#2 01. 11. 2015 22:19
Re: Operace s přirozenými čísly
Výhodná bývá úprava na součin, tady např.
odtud by už mělo jít vidět, že pro libovolné  nějaká vyhovující
nějaká vyhovující 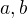 existovat budou.
existovat budou.
Obecněji se ptáš na řešitelnost rovnic v oboru přirozených (popř. celých nebo racionálních) čísel. Bohužel, obecná odpověď není možná a víceméně každá taková rovnice (říká se jí diofantická nebo diofantovská) vyžaduje indiviuální přístup.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#5 03. 11. 2015 01:00
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Operace s přirozenými čísly
Ahoj,
úpravami zjistíme, že jde vlastně o to vyjářit zlomek 1/n jako součet 1/a+1/b. Možná by pomohla teorie o kmenných zlomcích.
"Máte úhel beta." "No to nemám."
Offline
#6 03. 11. 2015 14:17
Re: Operace s přirozenými čísly
↑ krauva:
Kdysi jsem řešil "obrácenou úlohu" tedy pro zadané n spočítat to co navrhuje ↑ check_drummer:
tedy 1/n = 1/a+1/b
Program na tento výpočet si můžeš stáhnoutZde
Offline
#7 03. 11. 2015 17:32
Re: Operace s přirozenými čísly
Všetky riešenia vygenerujeme ľahko.
Ak  , tak
, tak  ,
,  , kde
, kde  . Potom
. Potom 
Zrejme však  , takže nutne
, takže nutne  , z čoho
, z čoho  . Potom
. Potom 
Všetky dvojice 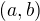 sa teda dajú napísať ako
sa teda dajú napísať ako  , kde
, kde  .
.
Z toho sa potom dajú ľahko robiť ďalšie úvahy o takých číslach...
1^6 - 2^6 + 3^6 = 666
Offline

 splňující
splňující  .
.