Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 11. 2015 13:12
programování
Napište program, který dostane na první řádce vstupu číslo N.
Na druhé řádce bude N čísel, které odpovídají celočíselným zbytkům po dělení čísel po řadě: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
A zrekonstruuje z ních původní číslo X, které je reprezentováno těmito zbytky.
Vaším úkolem je vypsat neznámé číslo X.
Příklad 1:
Vstup:
4
1 1 1 1
Výstup:
1
Příklad 2:
Vstup:
4
1 1 0 4
Výstup:
25
v Pascalu
Offline
- (téma jako vyřešené označil(a) misha2015)
#2 03. 11. 2015 13:56 — Editoval Formol (03. 11. 2015 13:57)
Re: programování
↑ misha2015:
Ahoj,
finta je jednoduchá. Označme si neznámé číslo X, zbytek po dělení prvočíslem p Rp a násobek prvočísla Mp. Pak jistě pro tvoje neznámé číslo platí: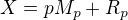
Když bude např. N=3, pak budeš mít soustavu rovnic: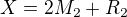

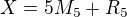
Protože Rp máš zadané, můžeš si to upravit do tvaru: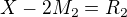
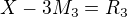
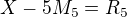
Tedy máš soustavu tří rovnic pro čtyři neznámé (X, M2, M3, M5). Pokud má taková soustava řešení, je jich nekonečně mnoho, vesměs neceločiselných. Podobně pro n prvočísel by soustava měla n+1 rovnic. Ještě taková poznámka, podle tvaru matice soustavy lze uhádnout, že bude mít řešení vždy.
Tak jak najít řešení? Nejlépe na papíře ;-) Řešení bude záviset na parametru. Parametr si zvolíme X. Pak pro neznámé Mp vyjde: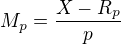
Tedy hledáš nejmenší takové celočíselné X, pro které je podíl 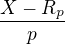 ve všech zvolených prvočíslech celočíselný. Tj. např. pokud zadáš N=2 a zbytky 1 a 2, tak hledáš nejmenší takové číslo, pro které budou celočíselné zlomky:
ve všech zvolených prvočíslech celočíselný. Tj. např. pokud zadáš N=2 a zbytky 1 a 2, tak hledáš nejmenší takové číslo, pro které budou celočíselné zlomky: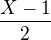
a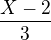
Ještě k otázce celočíselnosti toho zlomku. Nejsnazší způsob testování je prostě testovat zbytek po dělení čitatele jmenovatelem na nulovost.
(Šlo to trochu oklikou, ale jde mi o to, abys viděla, že ten myšlenkový postup není vůbec složitý.)
Доктор сказал «в морг» — значит в морг!
Offline
#3 03. 11. 2015 16:28
Re: programování
Zdravím,
vím že ti to asi na nic nebude, ale prostě mě to nedalo :-) :
Offline

