Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 11. 2015 18:11 — Editoval xstudentíkx (07. 11. 2015 18:14)
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
rozvinutí v periodický zlomek
Ahoj,
mám zde úlohu: Při základu 2 lze číslo  rozvinout v periodický zlomek s tříčlennou periodou:
rozvinout v periodický zlomek s tříčlennou periodou: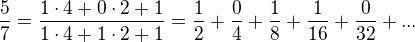
Pokud chci tímto způsobem rozložit jiný zlomek, třeba  o základu 2, nedaří se mi to, dostanu třeba
o základu 2, nedaří se mi to, dostanu třeba 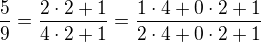 , ve jmenovateli se zřejmě nesmí násobit nulou, čemuž odporuje druhá možnost zápisu. Pokud tomu tak není, stejně se nedostávám k správným výsledkům.
, ve jmenovateli se zřejmě nesmí násobit nulou, čemuž odporuje druhá možnost zápisu. Pokud tomu tak není, stejně se nedostávám k správným výsledkům.
Offline
#2 07. 11. 2015 20:05
Re: rozvinutí v periodický zlomek
Ahoj ↑ xstudentíkx:,
Ako vysvetlis toto 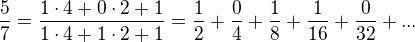 ?
?
Ja to automaticky nevidim.
Ako by som nasiel taky vysledok,
Delenim ako na ZS ake v dvojkovej sustave
5-->101
7-->111
A delenie v dvojkovej sustave da 0,101101101....
Ak to skusis z druhym zlomkom co ti to da?
Zo zlomkami kde mas menovatel 7 -->111 budes mat viacej uspechov.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 09. 11. 2015 13:56 — Editoval Honzc (09. 11. 2015 14:34)
Re: rozvinutí v periodický zlomek
↑ xstudentíkx:
Přečti si pozorně co ti napsal ↑ vanok: (zdravím)
Pak 
A tedy 
Aby se tento výsledek dal rozvinout do periody 3 lze použít tuto fintu: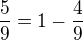
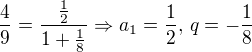
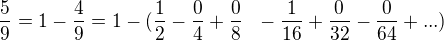
nebo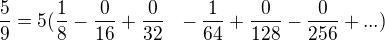
Offline
#4 09. 11. 2015 16:44
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: rozvinutí v periodický zlomek
Offline
