Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 11. 2015 00:23
matica zobrazenia
dobrý večer
potreboval by som pomoc s úlohou: nájdite všetky matice typu 2x3 nad 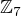 také, že pre príslušné zobrazenie
také, že pre príslušné zobrazenie  platia podmienky:
platia podmienky:
a 
potreboval by som hint, ako sa k tej matici dostať.
prvá podmienka je, že 
druhá, že pravé strany sú násobky vektoru 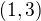 . no neviem sa pohnúť ďalej. za akúkoľvek radu vopred ďakujem .
. no neviem sa pohnúť ďalej. za akúkoľvek radu vopred ďakujem .
Per aspera ad astra
Offline
#2 09. 11. 2015 01:19
Re: matica zobrazenia
Ahoj,
stačí si to rozepsat. Obecnou matici si zvol například 
a zkrátka použij informace, které znáš. Daný příklad vede na nějaké parametry.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#3 09. 11. 2015 01:34
Re: matica zobrazenia
↑ Freedy:
ahoj
viem, že prvá podmienka mi dá niečo v zmysle  a
a  len netuším, ako to zakomponovať do druhej podmienky, tá by mala dať, že
len netuším, ako to zakomponovať do druhej podmienky, tá by mala dať, že

lenže je tam príliš veľa neznámych a neviem, či toto je správna cesta. ďakujem .
Per aspera ad astra
Offline
#4 09. 11. 2015 07:41
Re: matica zobrazenia
↑ vytautas:
ano, je to správná cesta. A problém s vícero proměnnýma by ti na mff nejspíš neměl vadit. Jelikož volná proměnná = parametr.
Zkrátka hledáš takovou matici, jejíž jádro je rovno (3,2,5)^T a obrazem libovolného vektoru je vektor t*(1,3)^T. Musí být tedy splněny obě podmínky najednou
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 09. 11. 2015 18:57
Re: matica zobrazenia
↑ Freedy:
povedzme, že 
tak si zoberiem  . vtedy dostanem práve
. vtedy dostanem práve  , čiže
, čiže 
keď zoberiem  dostanem, že
dostanem, že 
keď zoberiem  , dostanem
, dostanem 
a tak ďalej . z týchto dvoch dostanem rovnice 
a tak ďalej... a takže to mám vyriešiť pre  s koeficientami
s koeficientami  atď ?
atď ?
ďakujem za tvoj čas.
Per aspera ad astra
Offline
#6 09. 11. 2015 19:04
Re: matica zobrazenia
Ahojte, asi jsem fakt pitomá, ale vyjádřila jsem si to takto
pak jsem to vynásobila a vyšly mi čtyři rovnice, ty jsem nějak dala do dvou matic ale dál netuším.
Počet proměnných by nevadil, problém je v tom, že jsou "neznámé" i v koeficientech :/ Zkoušela jsem to počítat i pro nějaký určitý vektor, ale nikam to nevede :/
Nebylo by ještě nějaký nakopnutí ? Díky moc
Žít a nefilosofovat je jako mít zavřené oči a nikdy se ani nepokusit je otevřít. (Descartes)
Offline
#7 09. 11. 2015 19:06
Re: matica zobrazenia
↑ vytautas:
hmm, ako som si teraz všimol, rovnice pre  a
a  sú lineárne závislé, čiže budem mať rovnice
sú lineárne závislé, čiže budem mať rovnice  pre nejaké riešenie
pre nejaké riešenie  a vyriešim ich pre
a vyriešim ich pre  , chápem správne ?
, chápem správne ?
Per aspera ad astra
Offline
#8 09. 11. 2015 19:21
Re: matica zobrazenia
Netroufám si říct, že vaše postupy jsou špatné, nicméně mi přijdou zbytečně složité.
Dám vám dva příklady. Až je vyřešíte, dejte vědět a nastíním další postup.
1) najděte takovou matici A' typu 2×3, že platí Ker A = t(3,2,5)^T
2) najděte takovou matici A'' typu 2×3, že pro zobrazení  platí
platí 
Nicméně, domácí úkoly... jsou domácí úkoly... ty vás mají donutit, si danou látku pečlivě prostudovat a přijít na řešení částečně samostatně.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#9 09. 11. 2015 19:21
Re: matica zobrazenia
↑ vytautas: jo, to bych taky ráda věděla :) právě že uplně nevím jak je vyřešit
Žít a nefilosofovat je jako mít zavřené oči a nikdy se ani nepokusit je otevřít. (Descartes)
Offline
#11 09. 11. 2015 19:59
Re: matica zobrazenia
↑ vytautas: já jsem zase dostala a právě že taky nevím jak tyto dva problémy (hlavně ten druhý vyřešit)
a právě že taky nevím jak tyto dva problémy (hlavně ten druhý vyřešit)
Žít a nefilosofovat je jako mít zavřené oči a nikdy se ani nepokusit je otevřít. (Descartes)
Offline
#12 09. 11. 2015 20:34
Re: matica zobrazenia
↑ flowergo:
toto je správný tvar, nicméně je lepší jej vyjádřit parametricky.
Nyní najdi takovou matici, která splňuje druhou podmínku. To znamená takovou matici, že zobrazení určené touto maticí zobrazí libovolný vektor  do t-násobku vektoru (1,3)^T.
do t-násobku vektoru (1,3)^T.
Nakonec stačí tyto dvě podmínky sloučit
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#14 09. 11. 2015 21:03
Offline
#15 09. 11. 2015 21:10
Re: matica zobrazenia
řešila jsem tu obecnou matici krát  rovnou nulovemu vektoru (jakože t=1). Kdyby t=2,3,4... 6 tak ti vyjde úplně to samé :)
rovnou nulovemu vektoru (jakože t=1). Kdyby t=2,3,4... 6 tak ti vyjde úplně to samé :)
Žít a nefilosofovat je jako mít zavřené oči a nikdy se ani nepokusit je otevřít. (Descartes)
Offline
#16 09. 11. 2015 21:24
Re: matica zobrazenia
↑ flowergo:
chápem, len netuším, čo si presne spravila, keď riešiš tú maticu, tak dostaneš 2 rovnice o 6 neznámych a z toho neviem ako sa pohnúť.
Per aspera ad astra
Offline
#17 09. 11. 2015 21:29
Re: matica zobrazenia
↑ vytautas:
v tych dvoch rovniciach si vyjadrila acko a decko pomocou tych zvysnych premennych. pokial ti to nevychadza tak nezabudni ze sme v Z sedem.
Offline
#18 09. 11. 2015 21:30
Offline
#19 09. 11. 2015 21:47 — Editoval vytautas (09. 11. 2015 21:47)
Re: matica zobrazenia
↑ flowergo:
z druhej podmienky sa dá dostať:  možno to pomôže
možno to pomôže
Per aspera ad astra
Offline
#20 09. 11. 2015 23:17
Re: matica zobrazenia
↑ vytautas: no kdybych věděla jak to odsud dostat, tak by to pomohlo :D
pořád mám buď 
a buď tam prostě mám moc různejch neznámejch (jako v koeficientech) a dosadit tam nějaké vektory nepomáhá :/ mě lingebra fakt moc nedává smysl :'(
Žít a nefilosofovat je jako mít zavřené oči a nikdy se ani nepokusit je otevřít. (Descartes)
Offline
#21 09. 11. 2015 23:23
Re: matica zobrazenia
smysl to dává dokonalý.
Stačí vyřešit obě podmínky a potom je zkombinovat.
Něco na způsob
Čísla dělitelná dvěma se zapíšou x = 2n, kde n je celé. (1)
Čísla dělitelná třema se zapíšou x = 3n, kde n je celé. (2)
Chci číslo, které je dělitelné jak dvěma, tak třema. Co musím proto udělat? musí platit jak podmínka (1) tak (2).
Prostě si vyjádřete matici A', pak A'' a dostanete obě v závislosti na nějakých paramtrech. Ty parametry se posléze zredukují, jelikož na ně budete klást více nároků při té kombinaci.
Zkus si vymyslet nějakou matici Q, jejíž obrazem v zobrazení  bude vektor (t,3t)
bude vektor (t,3t)
Můžu ti dát takový hint, co třeba matice (1,3)^T nebo třeba
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#22 09. 11. 2015 23:58 — Editoval vanok (10. 11. 2015 14:21)
Re: matica zobrazenia
Ahoj ↑ Freedy:,
Dobra rada, a naviac upresni, ze tu sa pracuje v 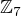
( pre zaujimavost, kolko prvkov ma jadro a kolko ich ma obraz tohto zobrazenia?)
Dalsia otazka : je iste, ze take zobrazenie moze vobec existovat?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

 tak za
tak za 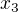 dosadím
dosadím 