Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 11. 2015 14:34 — Editoval patrik7741 (14. 11. 2015 16:48)
- patrik7741


- Příspěvky: 255
- Pozice: student
- Reputace: 2
Zákon zachovania hybnosti
Ahojte,mám tu takú úvahu, ak by do seba narazili dve telesa, a mali by sme vypočítať nejaky udaj, tak by sme počítali cez rovnicu
No a teraz tá moja uvaha , idu napriklad dve auta , istymi rychlostami a hmotnostami a narazia do seba, a teraz ma zaujima len vysledna rychlost a smer rychlosti len jedneho auta, ako to teda zakomponovať do tejto rovnice ??
Samozrejme uvažujeme dokonale nepružnú zrážku.
Ďakujem za všetky nápady
Aspoň si teda myslím. Pekný deň prajem :)
Offline
#2 15. 11. 2015 08:44
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Zákon zachovania hybnosti
Zdravím,
pokud uvažuješ dokonale nepružnou srážku, tak po srážce se pohybuji spolu stejnou rychlosti ve stejném směru (což asi u aut je trošku obtížné pro praktickou představu, lepší si představit plastelínové koule). Také je to vidět, když roznásobíš závorky napravo ve Tvé rovnici. Stačí tak? Děkuji.
Offline
#3 15. 11. 2015 09:35
- patrik7741


- Příspěvky: 255
- Pozice: student
- Reputace: 2
Re: Zákon zachovania hybnosti
↑ jelena:
Ďakujem, ešte ma zaujíma jedna vec, ked idu oproti sebe, bude ta rovnica vyzerat takto: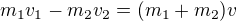
????
Alebo tam ma byt plus ?
Aspoň si teda myslím. Pekný deň prajem :)
Offline
#4 15. 11. 2015 11:28
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Zákon zachovania hybnosti
↑ patrik7741:
pokud zapisuješ ve vektorové formě, potom máš 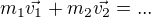 , při přepisu pro následný výpočet uvažuješ souřadný systém, ve kterém počítáš a projekce vektorů na zvolené osy. Nejspíš zvolíš osu shodnou s přímkou, po které se pohybuji obě auta, potom v projekci bude x-složka vektoru jednoho auta s plusem, druhého auta, co jede v opačném směru, s minusem, y-složky jsou nulové.
, při přepisu pro následný výpočet uvažuješ souřadný systém, ve kterém počítáš a projekce vektorů na zvolené osy. Nejspíš zvolíš osu shodnou s přímkou, po které se pohybuji obě auta, potom v projekci bude x-složka vektoru jednoho auta s plusem, druhého auta, co jede v opačném směru, s minusem, y-složky jsou nulové.
Ale není problém si zvolit souřadnice tak, že směr aut bude tvořit se souřadnici odchylku odlišnou od 0, potom uvažuješ projekce s ohledem na rozložení vektoru rychlosti. Pochopitelně, že vždy volíme souřadný systém tak, aby projekce byly co nejjednodušší.
Offline
#5 15. 11. 2015 11:34
- patrik7741


- Příspěvky: 255
- Pozice: student
- Reputace: 2
Re: Zákon zachovania hybnosti
↑ jelena:
ďakujem jelena :) Pozrela by si sa prosím ťa na môj druhý príspevok, kde som to použil pri riešení príkladu? Samozrejme, ak máš teda čas :) Pekný deň prajem
Aspoň si teda myslím. Pekný deň prajem :)
Offline
#6 15. 11. 2015 17:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Zákon zachovania hybnosti
↑ patrik7741:
také děkuji, v tom 2. tématu používáš směr těžšího tělesa proti kladnému směru osy x (v kladném směru jede první lehčí těleso). Jelikož po srážce projekce výsledné rychlosti je záporná, to znamená, že směr výsledné rychlosti souhlasí s původním směrem těžšího tělesa. Tedy nezměnilo směr.
Nechávám tento komentář v toto tématu, jelikož navazuje na vysvětlení ↑ příspěvku 4:, v druhém tématu je příklad konkrétního použití. Pokud je zájem, můžeš pohyb uspořádat tak, že v kladném směru pojede těžší těleso a zkontrolovat, zda "zachování směru" zůstává. Vždy, pokud počítáš úlohu, ve které vystupuje vektorová veličina, kresli k tomu souřadný systém.
Offline
#7 15. 11. 2015 18:25
- patrik7741


- Příspěvky: 255
- Pozice: student
- Reputace: 2
Re: Zákon zachovania hybnosti
↑ jelena:
ďakujem jelena, môžem teda okrem tejto veci so smerom , považovať moje riešenie za spravne ?
Aspoň si teda myslím. Pekný deň prajem :)
Offline