Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » neurčitý integrál s odmocninou (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 11. 2015 18:04 — Editoval krauva (26. 11. 2015 18:19)
neurčitý integrál s odmocninou
Ahojte,
potřeboval bych poradit, jak postupovat při určení následující primitivní funkce: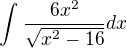
Chtěl jsem integrál upravit tak, aby šel použít arkussinus, ale to by muselo být pod odmocninou 16 a -x^2, žejo?
Děkuji za rady ;)
Offline
- (téma jako vyřešené označil(a) krauva)
#6 26. 11. 2015 23:50 — Editoval jelena (27. 11. 2015 00:01)
#7 27. 11. 2015 00:41
Re: neurčitý integrál s odmocninou
↑ krauva:
Ano, řekl bych, že to tak vychází, ale další řešení touto cestou zřejmě k ničemu zvlášť hezkému, jak jsem to zkusil, nepovede.
Kolegyně jelena jako lepší postup navrhuje per partes (což mě vůbec nenapadlo) - to zřejmě až ráno.
Pokud se tedy nemýlím.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » neurčitý integrál s odmocninou (TOTO TÉMA JE VYŘEŠENÉ)

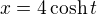 .
.
 (je to dobře?). Dále jsem perpartesoval, a zdá se mi, že to nikam nevede. Nebo vede?
(je to dobře?). Dále jsem perpartesoval, a zdá se mi, že to nikam nevede. Nebo vede?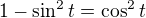 .
.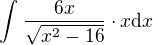 . Potom doplním v editu, jak to šlo (edit - asi bych tak postupovala).
. Potom doplním v editu, jak to šlo (edit - asi bych tak postupovala).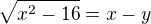 staci vyjadrit
staci vyjadrit 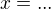 a z toho
a z toho 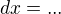 a ak sa nemylim tak dostaneme
a ak sa nemylim tak dostaneme