Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita fce s odmocninou. kontrola postupu (TOTO TÉMA JE VYŘEŠENÉ)
#7 27. 11. 2015 20:21
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita fce s odmocninou. kontrola postupu
Zdravím,
↑ jinsun: především je to značně nepřehledné - napravo od okna zprávy je Editor TeX, používej, prosím. Navíc, pokud klepneš na TeX zápisy kolegů, tak se přenesou do Tvé zprávy a můžeš pokračovat v úpravě nebo v zápisu.
Potřeboval jsi rozšíření do vzorce 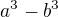 , postup viz kolega ↑ Al1:, Ty ovšem provádíš něco jiného, navíc není jasné, jak myšleno "škrtnutí" závorek
, postup viz kolega ↑ Al1:, Ty ovšem provádíš něco jiného, navíc není jasné, jak myšleno "škrtnutí" závorek 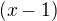 v posledním řádku. Zkus to, prosím, podle kolegy ↑ Al1:. Děkuji.
v posledním řádku. Zkus to, prosím, podle kolegy ↑ Al1:. Děkuji.
Offline
#8 27. 11. 2015 20:35
Re: Limita fce s odmocninou. kontrola postupu
↑ jinsun:
Zdravím,
tvá úprava není správná, na začátku druhého řádku ve zlomku krátíš, jenže chybně. V čitateli máš součet. Krátit výrazem (x-1) nelze. Je třeba výraz (x-1) vytknout a pak teprve krátit. Tím ovšem dostaneš úplně stejný výraz jako bylo zadání. Ve výpočtu této limity je nutné zvolit můj postup, nebo LH pravidlo.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita fce s odmocninou. kontrola postupu (TOTO TÉMA JE VYŘEŠENÉ)


![kopírovat do textarea $\lim_{x\to -1}{\frac{\sqrt[3]{-x}-\sqrt[3]{2+x}}{x+1}}=\lim_{x\to 1}{\frac{-x-(2+x)}{x^3+1}}$](/mathtex/21/21c7f52b1b5bf80ba34e75d7dbdbadb1.gif)

![kopírovat do textarea $\lim_{x\to -1}{\frac{\sqrt[3]{-x}-\sqrt[3]{2+x}}{x+1}}\cdot \frac{\sqrt[3]{(-x)^{2}}+\sqrt[3]{(-x)(2+x)}+\sqrt[3]{(2+x)^{2}}}{\sqrt[3]{(-x)^{2}}+\sqrt[3]{(-x)(2+x)}+\sqrt[3]{(2+x)^{2}}}=\ldots $](/mathtex/77/77a1cbe04ebe2e0cd604a317da1156ee.gif)
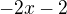 , které pokrátíš se jmenovatelem a potom již stačí dosadit.
, které pokrátíš se jmenovatelem a potom již stačí dosadit.