Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 11. 2015 16:54
Definiční obor derivace
Zdravím, mám jednu malou nejasnost u určování Df fce která se derivuje.
Zadání:
Derivování je ok (omlouvám se že to je printscreen), ale není mi jasné proč se ten definiční obor určuje jako nevčetně. Vždyť můžu odmocňovat nulu a definiční obor fce arccos(x) je od <-1;1>, tak proč tam jsou otevřené intervaly a ne uzavřené. Děkuji.
Offline
#2 29. 11. 2015 17:23 — Editoval Jenda358 (29. 11. 2015 17:29)
Re: Definiční obor derivace
Také zdravím.
Jako definiční obor původní funkce lze skutečně brát uzavřený interval ![$[0,4]$](/mathtex/63/63931f910184298db4d97021284cb279.gif "kopírovat do textarea")
. Derivace (myšleno oboustranná) však zjevně neexistuje přímo v bodech 0 a 4, takže jejím definičním oborem rozhodně nemůže být celý interval .
Ono ostatně i z toho výpočtu je vidět, že když se do té vypočtené derivace pokusíte dosadit číslo 0 nebo 4, dostanete nedefinovaný výraz (dělení nulou). Vyskytuje se tam totiž výraz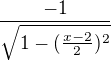 
.
Často se lze setkat s tím, že se celý uzavřený interval bere jako definiční obor derivace, přičemž v krajních bodech je to myšleno jako jednostranné derivace. V tomto případě nám však ani tento přístup nepomůže, neboť jednostranné derivace v bodech 0 a 4 jsou nevlastní.
Offline
#4 29. 11. 2015 17:39 — Editoval jinsun (29. 11. 2015 17:40)
Re: Definiční obor derivace
↑ Al1:↑ Jenda358:
Takže pokud bude v zadání:
tak zjišťuju Df pro tu 1. derivaci a ne pro "zadání" ?
edit: protože já to asi vždy dělal tak, že jsem nejdřív určoval Df a pak derivoval
Offline