Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Diofantická rovnice x^y=y^x (TOTO TÉMA JE VYŘEŠENÉ)
#1 24. 11. 2015 20:47 — Editoval zustajda (24. 11. 2015 20:50)
Diofantická rovnice x^y=y^x
Zadání: Najděte všechna kladná celá čísla x,y taková, že x<y splňující x^y=y^x
Našla jsem jednu dvojici čísel, pro kterou to platí: (2,4) a na internetu jsem se dočetla, že je tato dvojice jediná.
Žádám proto o radu, jak dokázat, že další řešení v celých číslech už neexistuje. Děkuji.
Offline
- (téma jako vyřešené označil(a) byk7)
#2 24. 11. 2015 23:47
- check_drummer

- Příspěvky: 4897
- Reputace: 105
Re: Diofantická rovnice x^y=y^x
↑ zustajda:
Ahoj, zkusil bych dokázat, že funkce f(x):=x^y-y^x chápaná jako funkce proměnné x je rostoucí (pro x>=2) a že řekněme od y:=5 a vyšší je f(2)>0 - takže nemůže být f(x)=0. (Je potřeba dořešit detaily a okrajové případy.)
"Máte úhel beta." "No to nemám."
Offline
#3 25. 11. 2015 00:11 — Editoval vanok (25. 11. 2015 11:25)
Re: Diofantická rovnice x^y=y^x
Ahoj ↑ zustajda:,
Mohla si najprv pozdravit, To by tu ostala krajsia stopa po tebe.
Riesenie sa da nast vdaka logaritmu povodnej rovnice.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Diofantická rovnice x^y=y^x (TOTO TÉMA JE VYŘEŠENÉ)





 ,
, 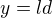 , kde
, kde  a
a  . Potom
. Potom  a
a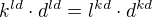

 , tj. aj pravá je deliteľná
, tj. aj pravá je deliteľná  , tak existuje prvočíslo
, tak existuje prvočíslo  deliace
deliace  . Potom ale toto prvočíslo delí
. Potom ale toto prvočíslo delí  , čo je spor s
, čo je spor s 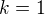 . Potom máme
. Potom máme .
. nemáme riesenie, keďže
nemáme riesenie, keďže  . Pre
. Pre 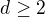 platí nerovnosť
platí nerovnosť  , pričom rovnosť nastavá len pre
, pričom rovnosť nastavá len pre  . To dáva riešenie
. To dáva riešenie  ,
,  .
.