Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » projekt č.6 4 příklad - Teorie grafů
#1 04. 12. 2015 12:24
- number4422

- Zelenáč
- Příspěvky: 2
- Škola: VSB-TUO
- Pozice: student
- Reputace: 0
projekt č.6 4 příklad - Teorie grafů
Mějme cestu 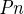 . Z této cesty budeme vybírat náhodně vždy dva různé vrcholy. Jaká bude střední hodnota vzdáleností náhodně vybraných dvojic vrcholů?
. Z této cesty budeme vybírat náhodně vždy dva různé vrcholy. Jaká bude střední hodnota vzdáleností náhodně vybraných dvojic vrcholů?
Rád bych se zeptal, jak toto zadání řešit? Již jsem si pročetl skripta ke středním hodnotám a teorii grafů, ale stále netuším kde začít. Potřeboval bych nějaký odrazový můstek, abych se měl čeho chytnout.
Děkuji
Offline
#2 04. 12. 2015 17:17
Re: projekt č.6 4 příklad - Teorie grafů
Zkuste si zahrát hru na cestě P_4. Náhodně vyberte dva vrcholy (třeba kostkou) a zapsat si, jaké délky měly cesty.
S jakou pravděpodobností trefíte celou cestu P_4?
Offline
#3 04. 12. 2015 22:15
- number4422

- Zelenáč
- Příspěvky: 2
- Škola: VSB-TUO
- Pozice: student
- Reputace: 0
Re: projekt č.6 4 příklad - Teorie grafů
↑ petrkovar: Velmi děkuji za odpověď. Pokud uvažuji správně, tak abych trefil celou cestu P_4 tak potřebuji náhodně vybrat v1 a v4. Pravděpodobnost, že vyberu první z nich je 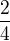 a pravděpodobnost, že vyberu ten druhý je
a pravděpodobnost, že vyberu ten druhý je  což je dohromady
což je dohromady  . To je v podstatě pravděpodobnost všech těch vrcholů, takže střední hodnotu počítám z těchto pravděpodobností?
. To je v podstatě pravděpodobnost všech těch vrcholů, takže střední hodnotu počítám z těchto pravděpodobností?
Offline
#4 06. 12. 2015 17:32
Re: projekt č.6 4 příklad - Teorie grafů
↑ number4422:Pravděpodobnost  je správně, ale postup nevypadá správně. Skoro bych řekl, že j správně náhodou. roč
je správně, ale postup nevypadá správně. Skoro bych řekl, že j správně náhodou. roč 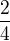 ?
?
Offline
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » projekt č.6 4 příklad - Teorie grafů