Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » důkaz - metrický prostor (troj. nerovnost) (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 12. 2015 23:19
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
důkaz - metrický prostor (troj. nerovnost)
Ahoj,
pracuji na důkazu a nemohu se hnout dále. Nebo spíš napadá mě mnoho kroků, ale většinou se dostávám k zbytečně obsáhlým zápisům. Prosím tedy někoho o nějaký nápad jak nerovnost dokázat v rozumném zápisu.
Offline
- (téma jako vyřešené označil(a) xstudentíkx)
#2 06. 12. 2015 23:38 — Editoval vanok (06. 12. 2015 23:40)
Re: důkaz - metrický prostor (troj. nerovnost)
Ahoj ↑ xstudentíkx:,
Mozes dokazat ekvivalentne, ze
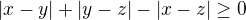
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 07. 12. 2015 12:37 — Editoval Rumburak (07. 12. 2015 12:39)
Re: důkaz - metrický prostor (troj. nerovnost)
↑ xstudentíkx:
Ahoj. (zdravím též kolegu ↑ vanok:).
Dokaž si nejprve jednodušší nerovnost 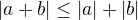 a tu pak použij při důkazu
a tu pak použij při důkazu
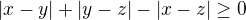 .
.
Offline
#4 07. 12. 2015 13:31
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: důkaz - metrický prostor (troj. nerovnost)
↑ vanok:, ↑ Rumburak:
Oběma děkuji, šla jsem na to zbytečně složitě :)
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » důkaz - metrický prostor (troj. nerovnost) (TOTO TÉMA JE VYŘEŠENÉ)
