#1 09. 12. 2015 21:19
Souvislost grafu
Zadání:
Je graf s 2n vrcholy a deg(v) = n souvislý?
(Redukované zadání z 2n kruhových objezdů, kde z každého vychází n ulic, a úkolem zjistit, je-li možné dostat se z libovolného objezdu na jiný libovolný objezd.)
Nevím proč, ale vyplývá z toho, že počet hran je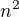 
s čímž už se nějak pracovat dá, protože 
(kde m je počet hran a n je počet vrcholů), můžu substituovat na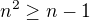 
. Což je vždy pravda a dalo by se to dokázat velmi jednoduše např. indukcí.
Jak se dostanu k počtu hran?
Díky
Offline
#2 10. 12. 2015 01:29
Re: Souvislost grafu
Uvedená argumentace není šikovná. proč 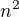? Nemělo by být alespoň ?
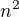Šikovnější je využít sporu (případně nepřímého důkazu).
Kdyby byl graf nesouvislý, kolik vrcholů by měla MENŠÍ komponenta?
Offline