Matematické Fórum

Crashatorr · 12. 12. 2015 14:53

Zdravím, poposil bych zda by ěnkdo mohl zkontrolovat můj postup
Je dána řada $\sum_{k=1}^{\infty }(1-x)x^{k},x\in \langle0,1\rangle$ , rozhodni o typu konvergence.
Pomocí limitního podílového kritéria vidím, že bude bodově konvergovat na $x\in \langle0,1\rangle$ , nyní pomocí Weierstrassova kritéria rozhodnu o stejnoměrné konvergenci
$|(1-x)x^{k}|\le |x^{k}|\le |\omega ^{k}|, \omega \in\langle0,1),x \in\langle0,\omega )$
$\sum_{k=1}^{\infty }\omega ^{k},\omega \in \langle0,1)$ konverguje, jedná se o geometrickou řadu, s q=omega.
Pak můžeme říct, že řada konverguje stejnoměrně na libovolném intervalu $\langle0,\omega )$ kde omega se blíží k jedničce čili na $\langle0,1)$

Bati · 12. 12. 2015 16:13

Ahoj ↑ Crashatorr:,
to je ok, ale tady se dá snadno argumentovat i bez Weirstrasse, protože pro $x\in(0,1)$ platí
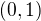$\sum_{k=1}^{\infty }(1-x)x^{k}=(1-x)\sum_{k=1}^{\infty }x^{k}=1$ , takže ta posloupnost je na $(0,1)$ dokonce konstantní.
Zatím jsi ještě neukázal, co se děje v jedničce (proč to nekonverguje stejnoměrně na [0,1]).

Crashatorr · 12. 12. 2015 16:36

↑ Bati:
No nebyl jsem si jistý jak to napsat, protože pro x vycházejí ty krajní hodnoty vždy nula takže to konvergenci neovlivní ale když tam zapojím omegu tak pro nulu to bude konvergovat ale pro jedničku ne.
Každopádně díky za tvůj postup, asi fakt beru kanón na vrabce, protože jsem také určoval pak součet a dělal jsem to přes derivace a integrace řady díky tomu, že stejnoměrně konverguje, vyšlo mi to stejně ale na 10 řádcích :D. Díky moc

Crashatorr · 12. 12. 2015 16:41

↑ Bati:
Nicméně ještě se dívám a když mám tu řadu od k=1 tak součet té geometrické řady cos psal je $\frac{x}{1-x}$ a když se mi pokrátí 1-x tak mi zbyde x nebo něco přehlížím?

Bati · 12. 12. 2015 16:48

↑ Crashatorr:
Jo, samozřejmě to má být $\frac{x}{1-x}$ , a tedy $x$ , to je ale pořád konstantní jakožto posloupnost funkcí.
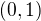Jestli je zadání $\sum_{k=1}^{\infty }(1-x)x^{k}$ , pak pro $x=1$ jsou přece všechny členy nulový, takže vyjde nula. Odtud dovodíš to, že nemůže být stejnoměrně spojitá na $[1-\varepsilon,1]$ , protože na $(0,1)$ se to chová jako $x$ , což jde k jedničce, ale nám vyšla nula. Tzn., že limitní funkce je nespojitá v 1 a posloupnost tedy nemůže stejnoměrně konvergovat.