Matematické Fórum

Freedy · 15. 12. 2015 18:34 — Editoval Freedy (15. 12. 2015 18:50)

Dobrý den,

mám trošku nejasnost v určování rychlosti růstu.
Když mám tyto dvě posloupnosti: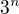
$3^n$ a ${2n\choose n}$ tak druhou přepíšu jako:
${2n\choose n}=\frac{(2n)!}{(n!)^2}\sim \frac{\sqrt{2\pi (2n)}(\frac{2n}{\text{e}})^{2n}}{2\pi n(\frac{n}{\text{e}})^{2n}}\sim 2^{2n}\frac{(\frac{n}{\text{e}})^{2n}}{\sqrt{n}(\frac{n}{\mathrm{e}^{}})^{2n}}\sim \frac{2^{2n}}{\sqrt{n}}=\mathrm{e}^{2n\ln 2-\frac{1}{2}\ln n}$ a tedy

${2n\choose n}=\text{exp}\bigg({2n\ln 2-\frac{1}{2}\ln n}\bigg)$
$3^n=\text{exp}(n\ln 3)$

Nyní když porovnám funkce v exponentech, dostávám:
$\lim_{n\to\infty }\frac{n\ln 3}{2n\ln 2-\frac{1}{2}\ln n}=\frac{\ln 3}{2\ln 2}$

Co mi toto řekne o původních dvou funkcích?
Jak z tohoto výsledku usoudím, že platí
$3^n=o\bigg({2n\choose n} \bigg)$ a ne třeba $3^n\sim ({2n\choose n} )$ ??
je to proto, protože limita vyšla v intervalu (0,1) ?
Takže platí něco jako, že při porovnání exponentů:
$\lim_{n\to\infty }\frac{f(n)}{g(n)}=A\in \langle0,1)$
posloupnost f(n) roste pomaleji než g(n)
$\lim_{n\to\infty }\frac{f(n)}{g(n)}=1$
rostou stejně
$\lim_{n\to\infty }\frac{f(n)}{g(n)}=B\in (1,\infty )$
f(n) roste rychleji než g(n) ??

A kdy tedy bude platit něco na způsob 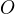$O$ popřípadě $\Theta$ ?

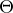Díky, freedy

Pavel · 15. 12. 2015 18:53

↑ Freedy:

Máš tam drobnou chybu, mělo by být ${2n\choose n}\sim \frac{2^{2n}}{\sqrt{\pi n}}=\frac{4^n}{\sqrt{\pi n}}$

Aby $3^n=o\bigg({2n\choose n} \bigg)$ , stačí ukázat $\lim_{n\to\infty}\frac{3^n}{{2n\choose n}}=0$ , což je triviální.

Freedy · 15. 12. 2015 19:11

Dobře, ale z toho mého tvaru, kde porovnávám exponenty, tak z toho nelze nic určit?
Ono totiž ne vždy je triviální porovnávat ty dvě posloupnosti jako limitu, například zde to ještě jde, ale když mám například
$n^{\sqrt{n}}$ a $\sqrt{n}^{n}$ .)

Mimochodem, jak bych srovnal
$\sum_{k=1}^{n}k!$ a $n^n$ ??

Díky

Pavel · 15. 12. 2015 20:05

↑ Freedy:

Pracuješ-li s podílem $f(x)/g(x)$ , pak v případě exponenciálních funkcí bys měl uvedené exponenty odečítat, nikoli dělit, tj. místo limity $\lim_{n\to\infty }\frac{n\ln 3}{2n\ln 2-\frac{1}{2}\ln n}$ by bylo vhodnější počítat limitu

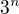$\lim_{n\to\infty }\left(n\ln 3-\left(2n\ln 2-\frac{1}{2}\ln n\right)\right)=-\infty$ . Tj. posloupnost $3^n$ je zanedbatetlná ve srovnání s posloupností ${2n\choose n}$

Chseš-li srovnat posloupnosti $\sum_{k=1}^{n}k!$ a $n^n$ , doporučují spočítat limitu

$\lim_{n\to\infty}\frac{\sum_{k=1}^{n}k!}{n^n}$

Pomůže Stolzova věta.

Freedy · 15. 12. 2015 20:11

aha, jasnýýý :D díky...

a já se divím, proč mi to tu pořád vychází tak hnusně -.-

Jinak tato limita je jednoduchá, to máš pravdu, dal by se použít i odhad
$\sum_{}^{}k!\le n\cdot n!\le (n+1)!\le n^n$ , ne?

Jinak díky za rady.
Freedy

Pavel · 15. 12. 2015 20:38

↑ Freedy:

Odhad je v pořádku, ale v této situaci nedává úplnou odpověď. Pokud bys jej použil, ukázal bys, že

$\lim_{n\to\infty}\frac{\sum_{k=1}^{n}k!}{n^n}\leq 1.$

Odtud by mohlo plynout jak $\sum_{k=1}^{n}k!=O\left(n^n\right)$ , tak i $\sum_{k=1}^{n}k!=o\left(n^n\right)$ .

Stolzova věta dává lepší výsledek:

$0\leq\lim_{n\to\infty}\frac{\sum_{k=1}^{n}k!}{n^n}&=\lim_{n\to\infty}\frac{n!}{n^n-(n-1)^{n-1}}\leq\lim_{n\to\infty}\frac{n!}{n^{n-1}-(n-1)^{n-1}}=\lim_{n\to\infty}\frac{\sqrt{2\pi n}\cdot n^n\cdot \mathrm e^{-n}}{n^{n-1}\left(1-\left(1-\frac 1n\right)^{n-1}\right)}=\\&=\lim_{n\to\infty}\frac{\sqrt{2\pi n}\cdot n}{\mathrm e^{n}\left(1-\left(1-\frac 1n\right)^{n-1}\right)}=0$

Takže $\sum_{k=1}^{n}k!=o\left(n^n\right)$ .

Freedy · 15. 12. 2015 20:45

Ano ano, se stolzovou větou souhlasím.
Nicméně, když tedy mám nějaké dvě funkce:
$f(n)=\mathrm{e}^{f_1(n)}$
$g(n)=\mathrm{e}^{g_1(n)}$
a chci je porovnat, tak zkoumám limitu
$\lim_{n\to\infty }f_1(n)-g_1(n)$
a teď rozlišuji:
$\lim_{}=-\infty$ potom
$f(n)=o(g(n))$
$\lim_{}=+\infty$
$g(n)=o(f(n))$
$\lim_{}=c\in R^+$
$f(n)=\Omega (g(n))$
$\lim_{}=c\in R^-$
$f(n)=O(g(n))$
$\lim_{}=0$
$f(n)\sim g(n)$

Ano?