Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 12. 2015 17:49 — Editoval Mauz (16. 12. 2015 17:52)
Průnik podprostorů
Zadání: Nechť V je lineární prostor všech matic typu 2x3 nad tělesem 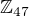 (s běžnými operacemi).
(s běžnými operacemi).
Jaká může být dimenze průniku podprostorů X a Y prostoru V, pokud zároveň platí:
a) X obsahuje čtyřprvkovou lineárně nezávislou posloupnost
b) Y nemá žádnou tříprvkovou množinu generátorů
Poznámka: Je třeba určit všechny možnosti, které mohou nastat, a odpověď dokázat.
Nějaká logika příkladu:
Nejdřív ohledně prostoru V:
Jeho báze bude vypadat tak, že se bude jednat o 6 matic typu 2x3, kde každá matice bude mít např. 1 na jednom místě a ostatních nuly tak, aby žádné dvě matice nebyli lineárně závislé. Taková posloupnost skutečně bazí prostoru V je, neboť pomocí ní jsme schopni získat jakoukoliv matici z V. Když máme bázi, máme dimenzi V a to dimV=6.
Teď prostor X:
Protože obsahuje 4-prvkovou lineárně nezávislou posloupnost, nemůže obsahovat ani 3-prvkovou(nebo dokonce s ještě nižším počtem prvků), ani 5-prvkovou(nebo dokonce s ještě vyšším počtem prvků) lineárně nezávislou posloupnost. Pro 3-prvkovou LN posloupnost, by muselo platit, že naše 4-prvková ze zadání by nebyla LN, neb jeden z jejích prvků by byl lineární kombinací prvků z 3-prvkové, což je však spor se zadáním. Podobně pro 5-prvkovou LN posloupnost, by musí platit, že jeden z jejích prvků je lineární kombinace prvků z 4-prvkové posloupnosti, což znamená, že není LN.
Proto má prostor X bázi právě 4, kde možných bazí je kombinace 4 prvků ze 6 (nezáleží na pořadí - báze (a,b) je stejná jako báze (b,a) nad nějakým tělesem), a to je 15.
Ze zadání ještě zbývá prostor Y:
Nemá ŽÁDNOU tříprvkovou množinu generátorů. To znamená:
1) Nemá množiny generátorů s 0, 1, 2 ani 3 prvky. Protože 3-prvkové množiny nám zakazuje zadání, nesmí zde být ani nižší, neboť např.: množina generátorů {(a,b)} 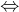 množina generátorů {(a,b),(5a,5b)}; nebo už né tak očividný příklad {(a,0,c), (0,b,c), (a,b,c)}
množina generátorů {(a,b),(5a,5b)}; nebo už né tak očividný příklad {(a,0,c), (0,b,c), (a,b,c)} 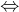 {(a,0,0), (0,b,0), (0,0,c), (a,5b,3c)}.
{(a,0,0), (0,b,0), (0,0,c), (a,5b,3c)}.
Množina generátorů "může" obsahovat LZ prvky.
2) Minimální množina generátorů obsahuje 4 LN prvky (plyne z 1) bodu).
3) Maximální množina generátorů s lineárně nezávislými prvky obsahuje 6 prvků (plyne z faktu, že se jedná o podprostor prostoru V).
(Pozn.: Množin generátorů obsahujících 4 LN prvky bude opět 15, obsahujících 5 LN prvků bude 6, obsahujících 6 LN prvků bude právě 1.)
To tedy znamená, že dimenze průniku podprostorů X, Y prostoru V je menší rovna 6 a vyšší rovna 4. 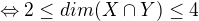
To jak bude vypadat ovlivní právě průnik prostorů X a Y. Bude 2 pro průnik, kde Y má pouze dva stejné prvky s X (čili Y bude obsahovat množinu generátorů obsahující 4 LN prvky a jen dva z nich náleží jak do Y, tak do X); 3 pro průnik, kde Y má právě tři stejné prvky s X (čili Y bude obsahovat množinu generátorů obsahující 4 nebo 5 LN prvků a právě tři z nich náleží jak do Y, tak do X); a 4 pro průnik, kde Y má právě čtyři stejné prvky s X (čili Y bude obsahovat množinu generátorů obsahující 4,5 nebo 6 LN prvků a právě čtyři z nich náleží jak do Y, tak do X).
Tak jo, někde nějaké chyby v argumentech? Připomínky? Poznámky? Chybějící odůvodnění?
Jestli ne, tak mi prosím alespoň poraďte, zdali tohle stačí jako struktura důkazu, nebo to potřebuje formálnější zápis.
Díky a promiňte za dlouhý post :)
PS: Jak je tam sakra relevantní to těleso??:O
Offline
#3 16. 12. 2015 19:44 — Editoval Pavel (16. 12. 2015 20:00)
Re: Průnik podprostorů
↑ Mauz:
Z Tvé úvahy mi není jasné, proč prostor X nemůže mít dimenzi vyšší než 4. Kdyby měl např. dimenzi 5, tak mezi 5 lineárně nezávislými vektory - taková pětice by vždy existovala - by byly libovolné čtyři z nich vždy lineárně nezávislé.
Větě
To tedy znamená, že dimenze průniku podprostorů X, Y prostoru V je menší rovna 6 a vyšší rovna 4
nerozumím. Průnik je menší nebo roven 6 a větší nebo roven 4 právě tehdy, když je průnik menší nebo roven 4 a větší nebo roven 2?
O dimenzi průniku pěkně pojednává věta o vztahu mezi dimenzemi jednotlivých podprostorů, dimenzi jejich průniku a jejich spojení (součtu).
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 16. 12. 2015 20:34
Re: Průnik podprostorů
Rovněž jako ↑ Pavel: nechápu, proč by podprostor X nemohl mít dimenzi větší než 4. Kdyby jeho dimenze byla 5, potom by jeho báze obsahovala 5 LN vektorů, to znamená, že určitě existuje posloupnost 4 prvků z X, která je LN.
Množinu Y jsi určil správně.
Platí tedy 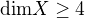
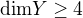
Nyní pokud chceš určit nejmenší možnou dimenzi tak stačí uvážit, že zvýšením dimenze podprostoru jistě dimenzi průnik nezmenšíš. Proto stačí uvažovat podprostory dimenze 4.
Když využiješ větu o dimenzi součtu a průniku dostaneš,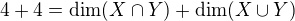 Aby byl člen
Aby byl člen 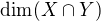 co nejmenší, musí být
co nejmenší, musí být 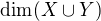 co největší. To nastane v případě, kdy
co největší. To nastane v případě, kdy 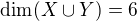 . To už si ověříš sám, zda-li takové podprostory X,Y mohou existovat. Potom je průnik 2, jak správně píšeš.
. To už si ověříš sám, zda-li takové podprostory X,Y mohou existovat. Potom je průnik 2, jak správně píšeš.
Když hledáš maximální možnou dimenzi průniku, stačí uvažovat opačně. Zvětšením dimenze určitě průnik nezmenšíš. Proto vezmeš maximální možnou dimenzi podprostorů a z věty o dimenzi součtu a průniku dostaneš: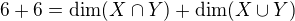 . Oba členy napravo mohou být maximálně 6, z toho již něco plyne.
. Oba členy napravo mohou být maximálně 6, z toho již něco plyne.
Nyní ti stačí ukázat, že dimenze 3 až 5 můžeš také najít.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 16. 12. 2015 22:09
Re: Průnik podprostorů
Jasně v té větě je chyba, TeXová verze je správně... má to tedy být:
To tedy znamená, že dimenze průniku podprostorů X, Y prostoru V je menší rovna a vyšší rovna ..TeX...
Úplně nechápu ten argument ohledně prostoru X...
Tedy možná trochu ano, ale raději bych se ujistil...
Kdyby bylo zadání:
a) X obsahuje jednoprvkovou lineárně nezávislou posloupnost
Tak např. X se může rovnat V (čili báze prostoru a podprostoru se rovnají <=> jedná o týž objekt), nebo opravdu může jeho dimenze být 1.
Takové zadání by otvíralo opravdu mnoho možností.
Ten můj argument byl prostě chybný, díky.
Asi jediný chybějící komponent jsou opravdu dimenze 3 a 5, ty předpokládám stačí konkrétně najít, nebo?
Díky mnohokrát za pomoc a zpětnou vazbu :3
Offline

 a
a  asi chceli dať
asi chceli dať