Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 12. 2015 21:17
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Operátor "podobný" derivaci
Ahoj.
(Předem upozorňuji, že některé pojmy níže jsou formulovány vágně, přesto věřím, že je zřejmé, co jsem jimi chtěl říci.) Zkoumal jsem, zda existuje nějaký operátor E, který by měl podobně "pěkné" vlastnosti jako operátor derivace D. Omezme se např. jen na polynomy s (řekněme) reálnými koeficienty (označme množinu těchto polynomů jako P), tj. D (a E) chápeme jako "funkci" z P do P. Operátor D má vhodné vlastnosti - lze pro f,g z P, c reálné, vyjádřit D(cf), D(f+g) a D(f.g) pomocí f,g,D(f),D(g) (konkrétně D(cf)=c.D(f), D(f+g)=D(f)+D(g) a D(f.g)=D(f).g+f.D(g)).
Hledejme operátor E s "podobnými" vlastnostmi jako D, tj. že E(cf), E(f+g) a E(f.g) lze vyjádřit pomocí f,g,E(f),E(g) (případně pomocí nějakých dalších jednoduchých funkcí závisejících na f,g). Operátor E by měl být "netriviální" a ani by se nemělo jednat o triviální modificaci D (např. E(f):=c.D(f) pro pevné číslo c je triviální modifikace D, rovněž nepovolíme volit E(f)=D(D(f)), ani nepovolíme E=D^{-1} (tj. E je operátor "integrace") apod.) Rovněž by se vztahu pro E(f+g) a E(f.g) neměla explicitně vyskytovat neurčitá x - tím eliminujeme "jednoduchá" E např. tvaru E(f):=x.f (a potom je E(f.g)=E(f).E(g)/x, čemuž se chceme vyhnout) - nebo alespoň povolme taková E, kde se x nevyskytuje ani v E(f) ani v E(f.g) (E(f+g), apod.) ve jmenovateli (tj. např. aby výaz vyjadřující E(f) byl polynomem v f,x a rovněž aby i výrazy vyjadřující E(f+g),E(f.g), apod. byly polynomy v E(f),E(g),x) - ale raději se těmto případům s výskytem x zcela vyhněme.
Pokoušel jsem se tedy hledat E "výrazně odlišný" od D, ale bez úspěchu. Např. hledejme E tak (ale není to nutné), aby se stupeň polynomu E(f) lišil (nejvýše) o 1 od stupně polynomu f. Máte nějaký nápad jak E sestrojit? (Znovu upozorňuji, že požadavky jsou formulovány poněkud vágně, ale snad je jasné, co jsem chtěl říci.) (Např. jsem zkoušel volit E tak, že bude  - ten je ovšem rovněž příliš "podobný" D.)
- ten je ovšem rovněž příliš "podobný" D.)
"Máte úhel beta." "No to nemám."
Offline
#2 16. 12. 2015 22:41
Re: Operátor "podobný" derivaci
↑ check_drummer:
Nabízí se použít místo derivace operátor diference, tj. 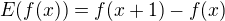 . I když i zde je podobnost s klasickou derivací.
. I když i zde je podobnost s klasickou derivací.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 17. 12. 2015 00:10
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Operátor "podobný" derivaci
↑ Pavel:
A podaří se potom vyjádřit E(f.g) bez odkazu na x? (Tj. jen pomocí f,g,E(f),E(g) bez použití např. E(f(x+1)), apod.)
"Máte úhel beta." "No to nemám."
Offline
#4 17. 12. 2015 00:20
Re: Operátor "podobný" derivaci
obvykle ked sa hovori o nejakej zovseobecnenej derivacii, tak sa ziadaju tieto vlastnosti
1) 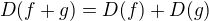
2) 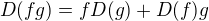
3) 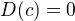 pre konstantu
pre konstantu 
a mozno este  kde tym x-om myslim identicku funkciu
kde tym x-om myslim identicku funkciu
preblem je ze na polynomoch to je uz dostatok vlastnosti na jednoznacne opisanie znmej derivacie
ale nejakym prirodzenym zovseobecnenim by mohla byt prave diferencia co Pavel spomina
s vlastnostami 1) a 3) by som moc nebabral - tak nam ostava 2)
skus preskumat co vsetko by ti dalo keby si mal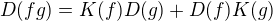 pricom by si ziadal
pricom by si ziadal 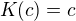 pre konstanty a teda aj klasicke
pre konstanty a teda aj klasicke 
Jedna moznost je teda ta diferencia  a
a ![kopírovat do textarea $K(f)=[f(x+1)+f(x)]/2$](/mathtex/c0/c0a15298e0250e92075c669057c80c00.gif) dalsia je trivialne derivacia; kde
dalsia je trivialne derivacia; kde  .
.
Offline
#5 17. 12. 2015 00:30
Re: Operátor "podobný" derivaci
↑ check_drummer:
Ano, podaří:
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 17. 12. 2015 00:32 — Editoval check_drummer (18. 12. 2015 16:56)
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Operátor "podobný" derivaci
↑ Brano:
Ahoj, já však netrvám na tom, aby šlo o derivaci (ať už zobecněnou, modifikovanou, apod.) - já hledám pouze operátor E (bez dalšího významu), pro který lze snadno vyjádřit E(f+g),E(f.g), jak o tom píšu výše. Tedy jde o zcela abstraktní objekt, ale i přesto, že nemám konkrétní požadavky na výraz vyjadřující E(f+g),E(f.g) (jen to, aby bylo možné je vyjádřit pomocí f,g,E(f),E(g) - nejlépe jako polynom v těchto veličinách), tak se mi takový E nedaří nalézt.
Teď mě napadlo, jesli by nebylo možné volit E tak, že obrátím pořadí koeficientů, tj. ai v f bude a(n-i) v E(f), zkusím to promyslet. (I když pak je E až zas moc symetrický :-)) A naví by se to dalo použít jen na polynomy do stupně nejvýše n, takže se vlastně nejedná přsně vzato o obrácení koeficientů, ale může jít i o zvýšení stupně...
Edit: je to špatně, součin nebude splňovat podmínky kladené na E.
"Máte úhel beta." "No to nemám."
Offline
#7 17. 12. 2015 00:38
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Operátor "podobný" derivaci
↑ Pavel:
E(f).E(g) asi odpovídá členu druhého řádu, který u běžné derivace vymizí, že?...
No ale i tak ten operátor příliš připomíná derivaci, i když zas ne úplně...
Akorát potom asi nebude vztah pro 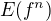 tak hezký jako u derivace, že? - u té je to
tak hezký jako u derivace, že? - u té je to 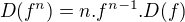 (Dokázat lze i formálně, nikoli odkazem na derivaci složené funkce.)
(Dokázat lze i formálně, nikoli odkazem na derivaci složené funkce.)
"Máte úhel beta." "No to nemám."
Offline
#8 10. 02. 2016 22:21
Re: Operátor "podobný" derivaci
Ahoj ↑ check_drummer:,
Mozno toto ta zaujme
https://en.m.wikipedia.org/wiki/Finite_difference
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
