Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » archimédovské pole - důkaz rac fcí (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 12. 2015 18:47
archimédovské pole - důkaz rac fcí
Ahoj,
nějak nemůžu pochopit následující důkaz, že pole rac fcí není archimédovské.
Ten důkaz je: vezměme  a
a 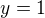 . Potom
. Potom  pro každé přirozené n.
pro každé přirozené n.
Není mi jasný, jaktože to platí pro každé n? Kdyby například n=1 tak mám 1/t a to je v bodě t=0,5 určitě větší než 1.
Offline
- (téma jako vyřešené označil(a) holyduke)
#4 18. 12. 2015 20:16
Re: archimédovské pole - důkaz rac fcí
↑ holyduke:
alespoň já tomu tak rozumím
Dva jsou tisíckrát jeden.
Offline
#6 19. 12. 2015 14:30
Re: archimédovské pole - důkaz rac fcí
↑ holyduke:
Je třeba si uvědomit, jak je definováno uspořádání v tělese racionálních funkcí. Nejedná se totiž o klasické uspořádání, které znáš z číselných oborů. To uspořádání funguje jinak.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#8 19. 12. 2015 16:20
Re: archimédovské pole - důkaz rac fcí
↑ holyduke:
Nechť  a
a  jsou dvě racionální funkce proměnné
jsou dvě racionální funkce proměnné  . Jak se v tělese racionálních funkcí definuje uspořádání
. Jak se v tělese racionálních funkcí definuje uspořádání  ? To je důležité si ujasnit, protože uvedená nerovnost nemá s funkčními hodnotami obou funkcí v nějakém bodě
? To je důležité si ujasnit, protože uvedená nerovnost nemá s funkčními hodnotami obou funkcí v nějakém bodě  (jak ses zmínil ve svém prvním příspěvku) nic společného.
(jak ses zmínil ve svém prvním příspěvku) nic společného.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#9 19. 12. 2015 17:51 — Editoval holyduke (19. 12. 2015 17:55)
Re: archimédovské pole - důkaz rac fcí
↑ Pavel:
Aha. Máme to definováno takto:
Je-li F uspořádané pole, pak na F nazveme ostré uspořádání takto: jestli-že
jestli-že  kde P je podmnožina F.
kde P je podmnožina F.
V mém případě tedy asi  pokud
pokud 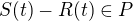 kde P bude nějaký výběr racionálních fcí?
kde P bude nějaký výběr racionálních fcí?
No a teď si nejsem jistý, ale mám v podstatě dvě možnosti, buď  nebo
nebo  (z definice uspořádaného pole). Takže když vezmu, že
(z definice uspořádaného pole). Takže když vezmu, že  ,
,  a
a  dostávám
dostávám  .
.
Je tohle dobrej začátek? Protože dál moc nevím, jak do toho zapojit to n-ko :/
Offline
#10 19. 12. 2015 18:25
Re: archimédovské pole - důkaz rac fcí
↑ holyduke:
A právě o tu podmnožinu  jde. Stačí pak ukázat, že
jde. Stačí pak ukázat, že 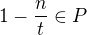 pro libovolné
pro libovolné 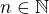 .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#11 19. 12. 2015 18:39
Re: archimédovské pole - důkaz rac fcí
↑ Pavel:
napadá mě tohle:
Nechť záporná celá čísla 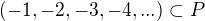 Pak podle definice uspořádaného pole platí
Pak podle definice uspořádaného pole platí  kde
kde 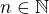 . Znovu podle definice uspoř. pole platí
. Znovu podle definice uspoř. pole platí  a tím dostáváme
a tím dostáváme  a tím je dokázáno, že Rac fce netvoří archimédovské pole.
a tím je dokázáno, že Rac fce netvoří archimédovské pole.
Může to tak být?
Offline
#12 19. 12. 2015 19:37
Re: archimédovské pole - důkaz rac fcí
↑ holyduke:
Každou racionální funkci lze vyjádřit ve tvaru
Pak
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#13 19. 12. 2015 19:56
Re: archimédovské pole - důkaz rac fcí
↑ Pavel:
A jak z toho vyplývá 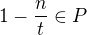 ?
?
ten můj ↑ holyduke: důkaz je špatně v čem?
Offline
#14 19. 12. 2015 20:20 — Editoval Pavel (19. 12. 2015 20:22)
Re: archimédovské pole - důkaz rac fcí
↑ holyduke:
Z Tvého důkazu není jasné, jaké kritérium musí racionální funkce splňovat, aby patřila do P. Je třeba nějak charakterizovat množinu P, aby se z toho daly vyvodit závěry pro konkrétní racionální funkce. Proč by např. mělo platit, že 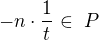 ? Navíc jestli dle Tvého do P patří záporná celá čísla, pak by podle definice uspořádaného pole měly do P patřít i jejich druhé mocniny, což jsou však čísla kladná.
? Navíc jestli dle Tvého do P patří záporná celá čísla, pak by podle definice uspořádaného pole měly do P patřít i jejich druhé mocniny, což jsou však čísla kladná.
---
To, že 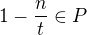 , vyplývá přímo vlastnosti, pomocí níž jsem P definoval.
, vyplývá přímo vlastnosti, pomocí níž jsem P definoval.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » archimédovské pole - důkaz rac fcí (TOTO TÉMA JE VYŘEŠENÉ)
