Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 12. 2015 19:34 — Editoval xxxxx19 (20. 12. 2015 19:40)
Limta s vnořeným cos( pi/2 cos(x))
Ahoj, nějakej hint na: ?
?
Pro 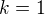 vychází
vychází  . Pro nižší myslim že je to
. Pro nižší myslim že je to  a pro vyšší
a pro vyšší  .
.
BEZ LOPITACE.
Díky za nápady.
Pokud naznačíte a já pochopim tak vložim kompletní řešení.
edit: Co nějak využít toho, že víme:
Offline
#2 20. 12. 2015 21:25
Re: Limta s vnořeným cos( pi/2 cos(x))
Ahoj,
k je přirozené? reálné? celé? komplexní?
Je lepší to nejprve specifikovat.
můžeš například postupovat takto.
Víš, že  tedy
tedy
nyní využiješ věty o limitě složené funkce a větu o aritmetice limit a dostaneš, že 

Tedy pro k = 1 máš požadovaný výsledek.
Pro k>1 sám usoudíš výsledek. Pokud je k celé, pak pro k<1 ihned výsledek také plyne.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#3 20. 12. 2015 21:49
Re: Limta s vnořeným cos( pi/2 cos(x))
Nakonec jsme to vyřešili podobně. Ale ještě bych varoval před tím závěrem. Navrhuji se omezit na Celočíselné k. Vzhledem k tomu, že tam nemáme něco jako  tak musíme rozlišit pro k<1 paritu.
tak musíme rozlišit pro k<1 paritu.
Poznamenejme, že původní příklad vypadal trochu jinak, takže tady jej uvádím celý.
Offline
#4 20. 12. 2015 22:00 — Editoval Freedy (20. 12. 2015 22:00)
Re: Limta s vnořeným cos( pi/2 cos(x))
Pokud bereš k celé, tak si to ale prohoď, protože pokud je k sudé, potom (k-1) je liché a tedy limita neexistuje. Pro k liché naopak existuje a je rovna +nekonečnu.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
