Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 27. 12. 2015 20:02 — Editoval krauva (27. 12. 2015 20:02)
Re: Rovnice a nerovnice
↑ Rorrina:
Zravím,
Takto řešit nelze. Nevíme, jestli je výraz, kterým násobíme, záporný či ne (kvůli změně nerovnosti). Vše se převede na jednu stranu a společného jmenovatele. Pak řešíme, kdy je výraz větší/menší než nula....
Offline
#4 27. 12. 2015 20:58 — Editoval misaH (27. 12. 2015 21:02)
- misaH
- Příspěvky: 13459
Re: Rovnice a nerovnice
↑ Rorrina:
Nie.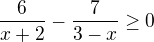
Teraz spoločný menovateľ.
Potom uvažovať, pre aké hodnoty premennej má zlomok požadovanú (nezápornú) hodnotu.
Upraviť čitateľ.
V NEROVNICI NESMIEŠ NÁSOBIŤ OBIDVE STRANY "PÍSMENOM", LEBO NEPOZNÁŠ Z N A M I E N K O.
Offline
#8 28. 12. 2015 07:54
- misaH
- Příspěvky: 13459
Re: Rovnice a nerovnice
↑ Rorrina: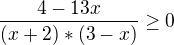
No a teraz nulové body a šup šup určovať znamienko zlomku...
Offline
#9 28. 12. 2015 15:25 Příspěvek uživatele Rorrina byl skryt uživatelem Rorrina.
#11 28. 12. 2015 16:53
- misaH
- Příspěvky: 13459
Re: Rovnice a nerovnice
↑ Rorrina:
To asi nie.
Nulové body sú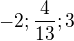
To poradie je dôležité.
Dosaď hocijaké čísla zo vzniknutých intervalov a sleduj znamienko zlomku.
Čitateľ môže byť 0, menovateľ nie.
Offline
#13 28. 12. 2015 18:46 — Editoval misaH (28. 12. 2015 19:41)
- misaH
- Příspěvky: 13459
Re: Rovnice a nerovnice
↑ Rorrina:
Ale veď tvoja úloha je zistiť, pre ktoré hodnoty je zlomok nezáporný. 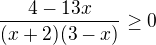
Mala by si si naštudovať základnú teóriu.
Takto komunikácia s tebou nemá význam.
Nulové body rozdelia číselnú os na 4 intervaly.
V každom z nich má zlomok niektoré znamienko +,-.
Podľa zadania ťa zaujíma, v ktorom intervale (pre čísla z ktorého intervalu) je zlomok kladný, prípadne rovný nule.
Offline
#15 28. 12. 2015 19:29 — Editoval misaH (28. 12. 2015 19:29)
- misaH
- Příspěvky: 13459
Re: Rovnice a nerovnice
↑ Rorrina:
Veru nie.
Naštuduj si konečne tú teóriu, toto nemá zmysel.
Veď si dosádzala nulové body - tak ako ti mohlo vyjsť + alebo mínus?
Intervaly sú 4.
Vieš ktoré sú to?
Offline
#16 28. 12. 2015 19:37
#18 28. 12. 2015 21:39 — Editoval misaH (28. 12. 2015 21:41)
- misaH
- Příspěvky: 13459
Re: Rovnice a nerovnice
↑ Rorrina:
Posledný stĺpec je znamienko celého zlomku.
Prvé tri stĺpce udávajú znamienko príslušného výrazu, ak dosadíš číslo z intervalu vľavo.
Intervaly sú tie 4, na ktoré delia číselnú os tie nulové body.
Tri mínusy napríklad znamenajú, že po násobení alebo delení troch záporných hodnôt má celý zlomok záporné znamienko.
Akú používaš učebnicu?
Offline












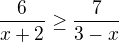
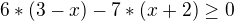
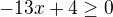

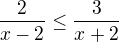
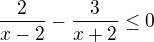
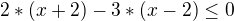
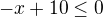

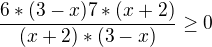
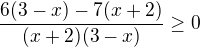
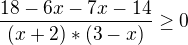
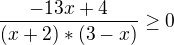
 (
(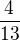 ,nekonečno)
,nekonečno)