Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 30. 12. 2015 23:54
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: limita
Je .
.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#3 30. 12. 2015 23:59
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: limita
Fígl je podívat se na to, že vnitřní cos jde k jedné, takže argument vnějšího cosu jde k pí/2, a to prostě (to je důležité :-)), a toto chování je podobné jako u sinu u nuly, kdy je vhodné sin srovnat s jeho argumentem. Ale tady máme cos, tak musíme ten srovnávací argument trochu upravit. Substitucí přes s odůvodněním přes prostotu přejdeme k standardní limitě podílu sin(t)/t. No a v druhém zlomku to zase po nějakém vytknutí pí/2 půjde na srovnání 1-cos(x) a x^2, no a teď podle toho, jaké bude "k", se to nakonec vyvine do vlastní nebo nevlastní limity.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#4 31. 12. 2015 00:10 — Editoval Brano (31. 12. 2015 00:31)
Re: limita
na taketo somariny treba pouzivat Taylorove rozvoje, lebo upravovanie funkcii je otrava a je fajn ked sa clovek uci zakladne pojmy a pocita lahke prikladiky a teda
a teda 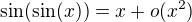 a teda
a teda 
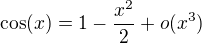 cize
cize 
a teda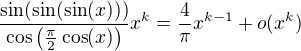
teda pre 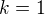 je ta limita
je ta limita  pre
pre  je nulova a pre
je nulova a pre  neexistuje.
neexistuje.
EDIT: k<1 treba este rozlisit parne (neexisuje) a neparne (nekonecno)
Offline
#5 31. 12. 2015 00:18
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: limita
Jo, tak to bych se měl taky ještě zamyslet, jestli jsem nepsal špatně to s nevlastními limitou.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#6 31. 12. 2015 00:27
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: limita
Myslím, že ono se to bude ještě lišit v případě k < 1 pro sudá a lichá k. Pro sudá limita existovat nebude - +-nekonečno z každé strany - a pro k lichá bude nekonečno.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#7 31. 12. 2015 00:30
#8 31. 12. 2015 00:32 — Editoval vytautas (31. 12. 2015 00:33)
Re: limita
↑ Sergejevicz:
ďakujem za reakciu, no stále mi nie je jasné ako prejsť od  k
k 
↑ Brano:
nemám zavedené Taylorove rozvoje, takže to nie je pre mňa "legal" postup pri písomke/skúške . Ďakujem aj tak.
Per aspera ad astra
Offline
#9 31. 12. 2015 00:47
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: limita
↑ vytautas:
Nejdřív použiješ substituci  . Tím se dostaneš (s odůvodněním přes prostotu y = y(x)) na
. Tím se dostaneš (s odůvodněním přes prostotu y = y(x)) na 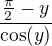 s limitěním pro y -> pi/2.
s limitěním pro y -> pi/2.
Pak použiješ to, že 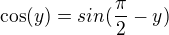 .
.
A pak opět VOLSF (věta o limitě složené funkce) s argumentem, že vnitřní funkce je prostá, jsi po substituci t = pi/2 - y v cíli :-).
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#10 31. 12. 2015 00:50
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: limita
Tedy ty se dostaneš na t/sin(t), ale to je 1/(sin(t)/t) a věta o vztahu limity a aritmetických operací tě pošle do cíle.
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
#11 31. 12. 2015 01:11
Offline
 kde
kde 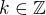
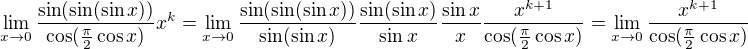
 prostá)
prostá)