Matematické Fórum

Freedy · 02. 01. 2016 14:53

Ahoj,

jelikož mě zatím nic nenapadá a už přemýšlím dost dlouho, tak bych rád poprosil o pomoc někoho zkušenějšího.
Jedná se o tuto limitu:
$\lim_{x\to0}\frac{\frac{2(1-\cos x)}{\sin x^2}-1}{x^2}$

Děkuji za popostrčení
Freedy

Al1 · 02. 01. 2016 14:58

↑ Freedy:

Zdravím,

zkus nahradit $\sin ^{2}x=1-\cos ^{2}x$ , dále rozklad na součin a krácení v prvním zlomku čitatele, A využít
$\lim_{x\to0}\frac{1-\cos x}{x^2}=\frac{1}{2}$

Freedy · 02. 01. 2016 15:01

↑ Al1:
taky zdravím

kdyby tam bylo $\sin ^2x$ tak bych ten příklad měl hotový za pár sekund jako spoustu dalších.
Bohužel tam je $\sin x^2$

Al1 · 02. 01. 2016 15:02 — Editoval Al1 (02. 01. 2016 15:09)

↑ Freedy:

Promiň, přehlédl jsem.

Tak nějak zamontovat $\lim_{x\to0}\frac{\sin x^{2}}{x^{2}}=1$

Freedy · 02. 01. 2016 15:11

↑ Al1:
zkoušel jsem i všelijaká rozšíření.
Bohužel nic k cíli zatím nevedlo -.-

vanok · 02. 01. 2016 18:43

Ahoj ↑ Freedy:,
Preco neskusis Taylorov rozvoj...(nasiel si limitu -1/12 ?)

Freedy · 03. 01. 2016 01:45

↑ vanok:
já okrajově tyto způsoby znám, ale jde mi o to spočítat tyto limity bez "cheatů".

Pavel · 03. 01. 2016 18:47 — Editoval Pavel (03. 01. 2016 19:01)

↑ Freedy:

Použijeme identitu

$\lim_{x\to 0}\frac{\sin x}{x}=1.$

a několik substitucí:

$\lim_{x\to0}\frac{\frac{2(1-\cos x)}{\sin x^2}-1}{x^2} &=\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^2\,\sin x^2} =\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^4}\\ &=\lim_{x\to0}\frac{2-2\cos x-x^2}{x^4}+\lim_{x\to0}\frac{x^2-\sin x^2}{x^4}\,.$

Substitucí $y=x^2$ vypočítáme druhou limitu:

$\ell :&=\lim_{x\to0}\frac{x^2-\sin x^2}{x^4} =\lim_{y\to0}\frac{y-\sin y}{y^2}\,.$

Dále položme $y=2t$ , pak

$\ell&=\lim_{t\to0}\frac{2t-\sin 2t}{4t^2} =\lim_{t\to0}\frac{t-\sin t\cos t}{2t^2} =\lim_{t\to0}\frac{t-t\cos t}{2t^2}+\lim_{t\to0}\frac{t\cos t-\sin t\cos t}{2t^2}\\ &=\lim_{t\to0}\frac{1-\cos t}{2t}+\lim_{t\to0}\frac{t-\sin t}{2t^2} =\lim_{t\to0}\frac{\sin^2t}{2t(1+\cos t)}+\frac 12\,\ell =\lim_{t\to0}\frac{\sin t}{2(1+\cos t)}+\frac 12\,\ell =\frac 12\,\ell.$

Tj. $\ell=0$ , a tedy

$\lim_{x\to0}\frac{x^2-\sin x^2}{x^4}=0.$

Pro původní limitu proto platí

$\lim_{x\to0}\frac{\frac{2(1-\cos x)}{\sin x^2}-1}{x^2} &=\lim_{x\to0}\frac{2-2\cos x-x^2}{x^4}\,.$

Položíme substituci $x=2v$ , pak

$\lim_{x\to0}\frac{\frac{2(1-\cos x)}{\sin x^2}-1}{x^2} =\lim_{v\to0}\frac{2-2\cos 2v-4v^2}{16v^4} =\lim_{v\to0}\frac{4\sin^2v-4v^2}{16v^4} =\lim_{v\to0}\frac{\sin^2v-v^2}{4v^4}:=L.$

Položíme substituci $v=2w$ , pak

$L&=\lim_{w\to0}\frac{\sin^22w-4w^2}{64w^4} =\lim_{w\to0}\frac{4\sin^2w\cos^2w-4w^2}{64w^4} =\lim_{w\to0}\frac{\sin^2w(1-\sin^2w)-w^2}{16w^4}\\ &=\lim_{w\to0}\frac{\sin^2w-w^2}{16w^4}-\lim_{w\to0}\frac{\sin^4w}{16w^4} =\frac 14\,L-\frac 1{16}\,.$

Z rovnice $L=\frac 14\,L-\frac 1{16}$ určíme, že

${\color{blue}\boldsymbol{\lim_{x\to0}\frac{\frac{2(1-\cos x)}{\sin x^2}-1}{x^2}=-\frac 1{12}\,.}}$

PS. Veškeré výpočty platí pouze za předpokladu, že vyšetřované limity existují a jsou vlastní.

Freedy · 03. 01. 2016 20:09

↑ Pavel:
wow... je vidět, že máš perfektní nadhled. Doufám, že podobné řešení vymyslím někdy samostatně.
Děkuji ;)

Sergejevicz · 03. 01. 2016 20:20

↑ Pavel:
Tohle je fakt hard-core :-).

nanny1 · 03. 01. 2016 20:37 — Editoval nanny1 (03. 01. 2016 20:42)

↑ Pavel: To je hezký postup, klobouk dolů, ale obávám se, že není korektní nahradit funkci $\sin x^2$ funkcí $x^2$ ... I když v tomhle případě to na výsledek nemá vliv. Stejně by ale také neměla vliv záměna těchto funkcí v čitateli a výpočet by se daleko zjednodušil. Ale v některých případech to na výsledek může mít vliv... Např. v definici $L$ - pokud by se tady úplně stejně udělalo $\sin v=v$ , potom by vyšlo $L=0$ . :(

byk7 · 03. 01. 2016 20:43

↑ nanny1:

Jestli narážíš na tuto úpravu
$\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^2\,\sin x^2} =\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^4}$
tak ta je úplně v pořádku, protože
$\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^2\,\sin x^2}=\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^2\,\sin x^2}\cdot\frac{\sin x^2}{x^2} =\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^4}$
(využilo se toho, že $\lim_{x\to0}\frac{\sin x^{2}}{x^{2}}=1$ )

nanny1 · 03. 01. 2016 20:58 — Editoval nanny1 (03. 01. 2016 21:05)

↑ byk7: V tom případě je to OK, ale chtělo to rozepsat, na první pohled to vypadalo jako nahrazení funkce. Zajímavé by bylo ještě dokázat, že $\ell$ a $L$ existují a jsou vlastní. :)

Sergejevicz

byk7 napsal(a):
↑ nanny1:
…
tak ta je úplně v pořádku, protože
$\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^2\,\sin x^2}=\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^2\,\sin x^2}\cdot\frac{\sin x^2}{x^2} =\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^4}$
(využilo se toho, že $\lim_{x\to0}\frac{\sin x^{2}}{x^{2}}=1$ )

Já bych si tedy rád ujasnil, jak je myšlen první krok. Já si to vykládám takhle:

$\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^2\,\sin x^2}= $\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^2\,\sin x^2}$=$
$$\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^2\,\sin x^2}$\cdot 1= $\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^2\,\sin x^2}$\cdot$\lim_{x\to0}\frac{\sin x^2}{x^2}$=$
$=\lim_{x\to0}$\frac{2-2\cos x-\sin x^2}{x^2\,\sin x^2}\cdot\frac{\sin x^2}{x^2}$=\dots$ ,
přičemž v posledním kroku jsem použil větu o vztahu limity a aritmetických operací, která má jisté předpoklady :-). Pro tento příklad musí první z limit v součinu existovat.

Chápu to takto správně? Protože ono je to trochu podobné tzv. částečnému limitění, což je operace ilegální :-).

Freedy · 04. 01. 2016 20:15

↑ Sergejevicz:
ono se to vynechává, protože to není podstatné pro výpočet.
Korektní by samozřejmě bylo to tam pořád nechávat a nakonec použít aritmetiku limit. Nicméně by ten výpočet pak byl o dost delší -.-
částečné limitění je něco jiného. Tady se jen neopisují známé limity.

Sergejevicz

Freedy napsal(a):
↑ Sergejevicz:
...částečné limitění je něco jiného.

Vím. Právě jsem psal, že je to tomu "trochu podobné" :-). Ale tedy trik je to dobrý. Myslím, že jsem ho zatím nikdy nepoužil, ani snad neviděl.

byk7 · 04. 01. 2016 20:19

↑ Sergejevicz: ↑ Freedy:

Já bych po výpočtu přidal poznámku, že všechny limity existují a jsou vlastní, proto všechny úpravy byly korektní. Stejně tak při použití l'Hospitala.

Freedy · 04. 01. 2016 20:27

Ano a všude nad rovnáse psát otazník, popřípadě "na dluh" a pak to smazat -.-

Pavel · 04. 01. 2016 20:54 — Editoval Pavel (04. 01. 2016 20:59)

↑ Sergejevicz:

Jde sice o detail, ale ta úprava byla myšlena takto:

$\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^2\,\sin x^2}&= \lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^4\,\frac{\sin x^2}{x^2}}= \lim_{x\to0}\left(\frac{2-2\cos x-\sin x^2}{x^4}\cdot \frac{x^2}{\sin x^2}\right)\\ &=\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^4}\cdot \lim_{x\to0}\frac{x^2}{\sin x^2} =\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^4}\cdot 1\\ &=\lim_{x\to0}\frac{2-2\cos x-\sin x^2}{x^4}=\dots$

↑ byk7:

Problém je v tom, že bez použití derivací lze dokázat existenci limit a jejich konečnost dost obtížně. Samotný vztah $L=\frac 14\,L-\frac 1{16}$ na to nestačí, klidně by z něj mohlo plynout, že $L=+\infty$ nebo $L=-\infty$ .

Sergejevicz

↑ Freedy:
Ono ale třeba věta o vztahu limity a aritmetických operací se právě takhle používá. Vlastně se nejdřív udělá ta operace a ta je odůvodněná až tím, že vyjde smysluplný výsledek. Když nevyjde, musíme se vrátit, větu "odpoužít" a zkusit udělat něco jiného. Ta věta zní, že ano, "za jistých předpokladů je napě. limita součinu součin limit, pokud má pravá strana rovnosti smysl". Takže on musí člověk vlastně tak nějak vidět na několik kroků dopředu, aby věděl, že ty ppravy nejsou nadarmo :-).

byk7 · 04. 01. 2016 21:14

↑ Pavel:

Rozumím tomu správně, že Váš postup není úplný? Tzn. existenci a konečnost je třeba ještě dořešit?

Pavel · 04. 01. 2016 21:28

↑ byk7:

Není, samozřejmě. Postup je správný pouze za předpokladu existence a konečnosti všech limit. To je zásadní slabina celé techniky. Bez derivací se to dokazuje velmi těžko. S použitím derivací je pro změnu zbytečné toto dokazovat, pro výpočet limity stačí použít l'Hospitalovo pravidlo, nebo Taylorovy rozvoje příslušných funkcí.

nanny1 · 05. 01. 2016 00:20 — Editoval nanny1 (05. 01. 2016 00:23)

Pavel napsal(a):
↑ byk7:

Není, samozřejmě. Postup je správný pouze za předpokladu existence a konečnosti všech limit. To je zásadní slabina celé techniky. Bez derivací se to dokazuje velmi těžko. S použitím derivací je pro změnu zbytečné toto dokazovat, pro výpočet limity stačí použít l'Hospitalovo pravidlo, nebo Taylorovy rozvoje příslušných funkcí.

V tom je ta potíž. :) Zajímavé je, že kdyby se provedla malá modifikace 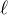$\ell$ , např. $\ell:=\lim\limits_{y\to 0}\frac{2y-\sin y}{y^2}$ , vyšel by výsledek úplně stejně, tj. $\ell=\frac{\ell}{2}$ , přesto tahle limita neexistuje.

Pavel · 05. 01. 2016 09:39

↑ nanny1:

To je přesně ono. Existence nějakého vztahu pro vyšetřovanou limitu ještě nezaručuje její existenci.

Matematické Fórum

#1 02. 01. 2016 14:53

limita

#2 02. 01. 2016 14:58

Re: limita

#3 02. 01. 2016 15:01

Re: limita

#4 02. 01. 2016 15:02 — Editoval Al1 (02. 01. 2016 15:09)

Re: limita

#5 02. 01. 2016 15:11

Re: limita

#6 02. 01. 2016 18:22 — Editoval kajzlik (02. 01. 2016 18:24) Příspěvek uživatele kajzlik byl skryt uživatelem kajzlik.

#7 02. 01. 2016 18:43

Re: limita

#8 03. 01. 2016 01:45

Re: limita

#9 03. 01. 2016 18:47 — Editoval Pavel (03. 01. 2016 19:01)

Re: limita

#10 03. 01. 2016 20:09

Re: limita

#11 03. 01. 2016 20:20

Re: limita

#12 03. 01. 2016 20:37 — Editoval nanny1 (03. 01. 2016 20:42)

Re: limita

#13 03. 01. 2016 20:43

Re: limita

#14 03. 01. 2016 20:58 — Editoval nanny1 (03. 01. 2016 21:05)

Re: limita

#15 04. 01. 2016 19:56 — Editoval Sergejevicz (04. 01. 2016 19:56)

Re: limita

byk7 napsal(a):

#16 04. 01. 2016 20:15

Re: limita

#17 04. 01. 2016 20:18 — Editoval Sergejevicz (04. 01. 2016 20:19)

Re: limita

Freedy napsal(a):

#18 04. 01. 2016 20:19

Re: limita

#19 04. 01. 2016 20:27

Re: limita

#20 04. 01. 2016 20:54 — Editoval Pavel (04. 01. 2016 20:59)

Re: limita

#21 04. 01. 2016 21:03 — Editoval Sergejevicz (04. 01. 2016 21:08)

Re: limita

#22 04. 01. 2016 21:14

Re: limita

#23 04. 01. 2016 21:28

Re: limita

#24 05. 01. 2016 00:20 — Editoval nanny1 (05. 01. 2016 00:23)

Re: limita

Pavel napsal(a):

#25 05. 01. 2016 09:39

Re: limita

Zápatí