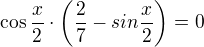Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 05. 01. 2016 19:03
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Goniometrická rovnice
↑ Rozárka96:
Na pravou stranu použij vzoreček
pro
Budoucnost patří aluminiu.
Offline
#3 05. 01. 2016 19:09
#4 05. 01. 2016 19:15
#5 05. 01. 2016 19:19
Re: Goniometrická rovnice
↑ Eratosthenes:
Zdravím,
nezdá se mi tvůj zápis, neboť pokud naznačuješ substituci  , pak by měla být zavedena v celé rovnici
, pak by měla být zavedena v celé rovnici 
Offline
#6 05. 01. 2016 19:20
Re: Goniometrická rovnice
↑ Eratosthenes:
ahá!
takže teď bych to mohla vydělit 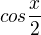 ?
?
Poté bych ten výraz upravila a měla bych  ?
?
Offline
#7 05. 01. 2016 19:27
Re: Goniometrická rovnice
↑ Rozárka96:
Zdravím,
výrazem 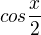 nesmíš dělit, musela bys napsat, že není roven nule, jenže tím bys přišla o řešení.
nesmíš dělit, musela bys napsat, že není roven nule, jenže tím bys přišla o řešení.
Zde tedy vše převeď na jednu stranu ( vytvoř tzv. homogenní rovnici), vytkni právě 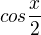 a řeš rovnici v součinovém tvaru.
a řeš rovnici v součinovém tvaru.
Offline