Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 01. 2016 23:07
Konvergence řady
Ahoj,
mohl by mi někdo prosím poradit, které kritérium se hodí na takovouto řadu? ;) kde
kde 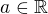
Není těžké určit, že  ani to, že pro a = 0 daná řada konverguje absolutně.
ani to, že pro a = 0 daná řada konverguje absolutně.
Nicméně mám problém s neabsolutní konvergencí -.-
Díky za nápady.
Freedy
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#3 06. 01. 2016 23:21
Re: Konvergence řady
Leibnizovo? :O vždyť to kalkuluje s (-1)^n a nerostoucí posloupností jdoucí k nule. Jak bych ho zde použil to fakt teda netuším -.-
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#4 06. 01. 2016 23:28 — Editoval Pavel (06. 01. 2016 23:29)
Re: Konvergence řady
↑ Freedy:
1. Dokaž, že 
2. Je jasné, že konvergence nezávisí na několika prvních členech řady. Ukaž, že od jistého  je
je  klesající posloupnost kladných reálných čísel s limitou rovnou nule.
klesající posloupnost kladných reálných čísel s limitou rovnou nule.
Leibniz pak situaci řeší.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 06. 01. 2016 23:46 — Editoval Freedy (06. 01. 2016 23:51)
Re: Konvergence řady
↑ Pavel:
tak dokázat 1 je snadné
2. takže stačí tedy ukázat, že pro velká n platí (protože sinus je v pravém okolí 0 rostoucí) následující: tedy
tedy
 a tedy
a tedy


 no ale toto přeci platí pro všechna
no ale toto přeci platí pro všechna 
Takže, je někde chyba? (mate mě to, že jsi naznačil "pro velká n")
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#9 07. 01. 2016 00:04
Re: Konvergence řady
↑ Freedy:
Je zřejmé, že  . Stačí pak najít takové
. Stačí pak najít takové  , že pro všechna
, že pro všechna  platí
platí  . Posloupnost bude pak kladná, klesající s limitou rovnou nule.
. Posloupnost bude pak kladná, klesající s limitou rovnou nule.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline


 větší než
větší než  a tam už sinus není rostoucí..
a tam už sinus není rostoucí..