Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 10. 01. 2016 00:58
- Sergejevicz


- Příspěvky: 581
- Škola: Mgr. mat. a fyz. modelování na MFF UK v r. 2014
- Pozice: výpočtář
- Reputace: 21
- Web
Re: kombinační číslo
↑ Freedy:
Myslel jsi kombinační číslo, ne faktorial, viď? :-).
A co použít Gamma funkci?
Kopáček: Mat. anal. nejen pro fyziky, Veselý: Zákl. mat. anal., Bečvář: Lin. alg., Matfyzpress
Bican: Lin. alg. a geom., Academia
Offline
 ? Vyčíslení podle vzorce by zahrnovalo faktoriál (1/2)! , který učit nedokážu. Wolfram mi přitom píše výsledek -(1/8), takže to nějak jde. Děkuji za radu.
? Vyčíslení podle vzorce by zahrnovalo faktoriál (1/2)! , který učit nedokážu. Wolfram mi přitom píše výsledek -(1/8), takže to nějak jde. Děkuji za radu. je pro
je pro  a
a 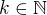 definován takto:
definován takto:
