Matematické Fórum

Freedy · 09. 01. 2016 23:13 — Editoval Freedy (10. 01. 2016 00:30)

Ahoj,

mohl by jste mi někdo poradit, kterým směrem se ubírat?:
Uvažuji množinu Q která je podmnožinou množiny všech sudých permutací na n prvcích (označím $R_n$ ).
Jak ukážu, že
$\forall \psi \in Q,\forall \omega \in R_n,\exists \lambda \in R_n \setminus Q:\omega\psi =\lambda \omega$
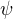(kde $\omega \psi$ znamená složení permutací kde $\psi$ je vnitřní permutace)

To, že nedostanu lichou permutaci je zřejmé. Jde mi však o to, jestli najdu vždycky takovou permutaci, která není obsažena v Q (tzn. chci ukázat, že Q=Rn)

Díky
Freedy

vanok · 10. 01. 2016 02:35

Ahoj ↑ Freedy:,
Co mozes povedat o
$\omega\psi \omega ^{-1}$

Brano · 10. 01. 2016 02:38

inymi slovami chces dokazat tvrdenie, ze pre lubovolne $\psi\in Q$ a $\omega\in R_n$ plati $\omega\psi\omega^{-1}\not\in Q$

co ale vo vseobecnosti neplati: uvaz napr. taku $Q$ co obsahuje $id$ a zober $\psi=\omega=id$ a potom $\omega\psi\omega^{-1}=id\in Q$ - spor.

Freedy · 10. 01. 2016 11:49 — Editoval Freedy (10. 01. 2016 11:50)

↑ vanok:
Ahoj tak muzu o ni rict to, ze bude mit stejny pocet cyklu stejne delky. Jak ukazat, ze nejaka konjugovana permutace lezi v Rn\Q zatim nevim.
Zkratka potrebuji zjistit, zda-li kdyz vezmu libovolnou permutaci z Q a okonjuguju ji permutaci z Rn tak muzu dostat permutaci z Rn\Q. Tzn ukazat uzavrenost konjugovani na Q.

↑ Brano:
Ahoj
To praveze vim. Nejake permutace budou v Q, nektere ale ne. Ja potrebuji ukazat, ze ty nektere tam opravdu nejsou a lze je ziskat okonjugovanim permutace z Q permutaci z Rn

Brano · 10. 01. 2016 22:43

↑ Freedy:
v tom pripade napis tvrdenie ktore potrebujes dokazat, lebo to co si napisal neplati - dal som kontrapriklad.
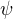da sa najst este silnejsi kontrapriklad; totizto to tvoje tvrdenie plati iba pre $Q=\emptyset$ , lebo ak $Q$ obsahuje vobec nejaky prvok $\psi$ tak ked zoberies $\omega=id$ tak $\omega\psi\omega^{-1}=\psi\in Q$

predpokladam, ze si chybne napisal kvantifikatory; tak si ich skontroluj.

Freedy · 10. 01. 2016 23:39

Kvantifikátory jsou v pořádku. Bohužel jsem zapomněl napsat ještě jeden předpoklad.

Kdyby byly kvantifikátory takto:
$\forall \psi \in Q,\forall \omega \in R_n,\exists \lambda \in R_n \setminus Q:\omega\psi =\lambda \omega$
tak bych mohl říct, že $Q=\{id\}$ a pak zcela určitě platí, že $\lambda \in Q$ protože:
$(\omega )(id)(\omega )^{-1}=id$ tedy by tvrzení neplatilo, protože lambda bude vždy z Q.

Takže podmínka na Q je, že obsahuje nějakou neidentickou permutaci.

vanok · 11. 01. 2016 00:47

Ahoj
Ak dobre rozumiem, to co si napisal tu ↑ Freedy:,
znamena ( po malom doplneni ), ze $\psi$ a $\lambda$ maju ten isty typ.
Je iste ze obe permutacie su parne....

Ani ja nerozumiem, ako aj Brano, na co chces pouzit Tvoju vetu. Aky je Tvoj ciel?

Brano · 11. 01. 2016 00:53 — Editoval Brano (11. 01. 2016 00:55)

↑ Freedy:
tak skusme este raz:
ak si oznacime $T:= [\forall \psi \in Q,\forall \omega \in R_n,\exists \lambda \in R_n \setminus Q:\omega\psi =\lambda \omega]$
tak potom plati $T\Rightarrow [Q=\emptyset]$
alebo si mozes napisat aj obmenu $[Q\not=\emptyset]\Rightarrow \neg T$

Freedy · 11. 01. 2016 01:26 — Editoval Freedy (11. 01. 2016 01:27)

↑ Brano:
Q je neprázdná (obsahuje neidentickou permutaci)

↑ vanok:
cíl je, dokázat, že Q se rovná Rn.
Tedy chci, aby platilo:
$\forall \psi \in Q,\forall \omega\in R_n:\omega \psi \omega ^{-1}\in Q$
Tedy najít takovou množinu Q aby byl tento výrok pravdivý + Q obsahuje neidentickou permutaci.
A nevím jak se dopracovat k tomu, že jediná taková množina bude Q=Rn

Brano · 11. 01. 2016 14:39

Ak je Q neprazdna tak potom T neplati - na to som ti tam napisal tu obmenu.

Ale uz sa asi dostavame k jadru problemu a to je, ze tym ze T neplati sa nic nedozvies o tom co chces dokazat. A zrejme je to tak ako som si myslel, ze si uviedol nespravne kvantifikatory.

Totizto ak chces dokazat vetu:
$\forall \psi \in Q,\forall \omega\in R_n:\omega \psi \omega ^{-1}\in Q\Rightarrow Q=R_n$
a chces to v podstate robit obmenou, tak dokazujes
$Q\not=R_n\Rightarrow \exists \psi \in Q,\exists \omega\in R_n:\omega \psi \omega ^{-1}\not\in Q$
(plus teda este treba v predpokladoch tu neprazdnost Q)

to je sposobene tym, ze negacia sa chova takto: $\neg[\forall x P(x)]\Leftrightarrow\exists x[\neg P(x)]$ .

Freedy · 11. 01. 2016 15:41

↑ Brano:
ano tento zápis:
$\forall \psi \in Q,\forall \omega\in R_n:\omega \psi \omega ^{-1}\in Q\Rightarrow Q=R_n$
jsem měl uvést již na začátku.
Nicméně je to potřeba ještě opatřit podmínkou, že Q obsahuje neidentickou permutaci, tedy $\exists \varkappa \in Q,\varkappa \not =id$ .
Nyní už je ta implikace pravdivá?
A pokud ano, jakým směrem vést důkaz?

Jinak se omlouvám, že jsem hned na začátku neuvedl správný zápis.

Brano · 12. 01. 2016 00:00

A zrejme asi predpokladas, ze Q je grupa - totizto ak by nemusela byt tak potom by si mohol pre nejake fixne
$\psi\in R_n$ take ze $\psi\not=id$ zobrat mnozinu $Q_\psi=\{\omega\psi\omega^-{1};\omega\in R_n\}$ a lahko sa presvedcis, ze $id\not\in Q_\psi$ .

Freedy · 12. 01. 2016 07:44

↑ Brano:
ano máš pravdu, $\forall \psi ,\varphi \in Q:\psi \varphi \in Q$

vanok · 12. 01. 2016 11:14

↑ Brano:,
Ahoj, To je pravda pokial ide o permutacie co nekomutuju.

Brano · 12. 01. 2016 12:40 — Editoval Brano (12. 01. 2016 12:41)

↑ vanok:
aj ked komutuju tak tam $id$ nevyrobime - to mal byt kontrapriklad, cize inymi slovami mnozina $Q$ co nie je cele $R_n$ a obsahuje neidenticku permutaciu a splna danu vlastnost.

↑ Freedy:
nejak sa nam tu zle komunikuje; pytam sa "je to grupa ?" a ty odpovedas "ano je to pologrupa" :)

tak ci tak sa da najst kontrapriklad aj keby to mala byt grupa
teda pre $n=1,2$ obsahuje $R_n$ iba identitu tak tam ziaden kontrapriklad nenajdeme. $R_3$
je izomorfna so 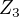$Z_3$ co je cyklicka grupa ktorej oba neidenticke prvky su generatory; takze tam to tvrdenie urcite plati. Ale uz $R_4$ ma podla wikipedie normalnu vlastnu podgrupu $Q=\{(),(12)(34),(13)(24),(14)(23)\}$ .
To, ze je to podgrupa sa overi lahko a to, ze je normalna (t.j. ta tvoja vlastnost) som neoveroval, ale verim wikipedii a nebolo by to tazke, len si to treba porozpisovat.

vanok · 12. 01. 2016 13:16 — Editoval vanok (12. 01. 2016 13:18)

Ahoj Brano
No ja som myslel na tuto vladnost [ re]p501190|Freedy[/re].

Inac $R_4$ Je jedina $R_n$ n>2 co nie je simple (jednoducha?)

Brano · 12. 01. 2016 17:18

↑ vanok:
vyzera, ze je to tak ako hovoris. Co by teda znamenalo, ze ak naozaj predpokladame, ze Q je grupa, tak to tvrdenie je pravdive pre vsetky $n\not=4$ - a pre $n=4$ je jediny kontrapriklad to co som uviedol.

Freedy · 12. 01. 2016 18:41

↑ Brano:
↑ vanok:
achjo... přijde mi že jsem se pustil do tématu, které nejsem schopný sám sledovat :D
Ano, pro n<= 4 to neplatí. Pro 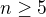$n\ge 5$ už to platí.

Grupa ani pologrupa zatím nevím co znamená. Ty permutace mají být uzavřené na skládání z Q (což není těžké dokázat, že jsou).
Myslím, že to zkusím ještě prostudovat, protože se jaksi nechytám :D

Matematické Fórum

#1 09. 01. 2016 23:13 — Editoval Freedy (10. 01. 2016 00:30)

permutace -.-

#2 10. 01. 2016 02:35

Re: permutace -.-

#3 10. 01. 2016 02:38

Re: permutace -.-

#4 10. 01. 2016 11:49 — Editoval Freedy (10. 01. 2016 11:50)

Re: permutace -.-

#5 10. 01. 2016 22:43

Re: permutace -.-

#6 10. 01. 2016 23:39

Re: permutace -.-

#7 11. 01. 2016 00:47

Re: permutace -.-

#8 11. 01. 2016 00:48 Příspěvek uživatele vanok byl skryt uživatelem vanok. Důvod: Duplicita

#9 11. 01. 2016 00:53 — Editoval Brano (11. 01. 2016 00:55)

Re: permutace -.-

#10 11. 01. 2016 01:26 — Editoval Freedy (11. 01. 2016 01:27)

Re: permutace -.-

#11 11. 01. 2016 14:39

Re: permutace -.-

#12 11. 01. 2016 15:41

Re: permutace -.-

#13 12. 01. 2016 00:00

Re: permutace -.-

#14 12. 01. 2016 07:44

Re: permutace -.-

#15 12. 01. 2016 11:14

Re: permutace -.-

#16 12. 01. 2016 12:40 — Editoval Brano (12. 01. 2016 12:41)

Re: permutace -.-

#17 12. 01. 2016 13:16 — Editoval vanok (12. 01. 2016 13:18)

Re: permutace -.-

#18 12. 01. 2016 17:18

Re: permutace -.-

#19 12. 01. 2016 18:41

Re: permutace -.-

Zápatí