Matematické Fórum

Ondrik_B · 19. 01. 2016 11:44

Ahoj, resim tento priklad:
//forum.matweb.cz/upload3/img/2016-01/00171_limita.jpg

Jmenovatel jsem zkousel rozsirit, ale nikam me to stejne nedovedlo. Prosim o nejakou radu.

Dik y.

Rumburak

↑ Ondrik_B:

Ahoj.

Šlo by to snadno přes binomický rozvoj:

$(1 + x)^a = \sum_{k=0}^{\infty}{a \choose k} x^k$ , pokud $|x| < 1$

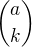kde ${a \choose k}$ jsou kombinační čísla zobecněná i pro případy, kdy číslo $a$ není nutně přirozené.
Pro přirozené číslo $a$ odtud dostáváme klasickou binomickou větu.

Ondrik_B · 19. 01. 2016 12:27

↑ Rumburak:
Dekuji za odpoved. Chtel bych se zeptat proc tam musi byt ta podminka $|x| < 1$

Rumburak · 19. 01. 2016 13:08

↑ Ondrik_B:
Aby byla zajištěna konvergence příslušné nekonečné řady, jejíž poloměr konvergence je 1.

Matematické Fórum

#1 19. 01. 2016 11:44

Limita

#2 19. 01. 2016 12:08 — Editoval Rumburak (19. 01. 2016 12:08)

Re: Limita

#3 19. 01. 2016 12:27

Re: Limita

#4 19. 01. 2016 13:08

Re: Limita

Zápatí