Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 01. 2016 00:15
challenge
Pozdravujem,
Citanie jednej knihy mi inspirovalo tento problem.
Nech cislo x je take ze 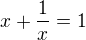
Najdite 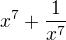 bez toho aby ste vypocitali cislo x
bez toho aby ste vypocitali cislo x
Ano je to mozne vyriesit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 26. 01. 2016 12:13
Re: challenge
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#3 26. 01. 2016 12:25
Re: challenge
↑ Freedy:
Provedl jsi důkaz implikace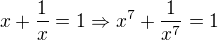 . A teď ti ukážu, jak bych to samé dokázal já:
. A teď ti ukážu, jak bych to samé dokázal já:
Offline
#6 26. 01. 2016 18:40
Re: challenge
Ahoj ↑ Bati:,
Vsak ano, to preto aby riesitel uvazoval vsetki mozne situacie.
No challenge.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 28. 01. 2016 19:59 — Editoval vanok (28. 01. 2016 20:22)
Re: challenge
Pozdravujem,
Este aj je jednoduche ukazat
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 31. 01. 2016 19:08 — Editoval vanok (01. 02. 2016 03:24)
Re: challenge
Pridam este odpoved na ↑ vanok:,
Skutocne mame postupne
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 21. 02. 2016 22:51 — Editoval vanok (21. 02. 2016 22:51)
Re: challenge
Na koniec este poznamka.
Asi kazdy si vsimol, ( ak pozna pojem grupy), ze  tvori cyklicku grupu pre nasobenie majucu 6 prvkov.
tvori cyklicku grupu pre nasobenie majucu 6 prvkov.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline



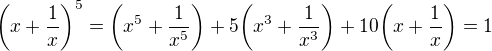




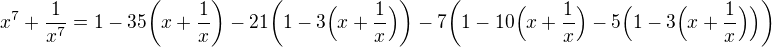
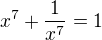
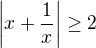 pro všechna x, takže zřejmě
pro všechna x, takže zřejmě  , a tedy implikace platí. :)
, a tedy implikace platí. :)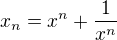 .
.  ,
, 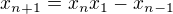 , tj.
, tj.  .
. 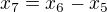


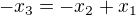


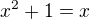
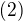
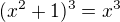
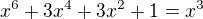
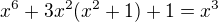 co da vdaka
co da vdaka