Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 01. 2016 18:36
hra s mincí
Hrajeme následující hru:
Házíme stále dokola mincí. Kdykoliv nám padne  -krát za sebou panna, můžeme si vybrat výhru typu
-krát za sebou panna, můžeme si vybrat výhru typu  (a začínáme počítat zase od 0), nebo můžeme prostě pokračovat v házení a čekat na lepší výhru. Když nám ovšem padne orel, tak se série pannen přeruší aniž bysme cokoliv získali (ale házíme dál).
(a začínáme počítat zase od 0), nebo můžeme prostě pokračovat v házení a čekat na lepší výhru. Když nám ovšem padne orel, tak se série pannen přeruší aniž bysme cokoliv získali (ale házíme dál).
Otázka zní: Kolik je průměrně potřeba hodů k získání jedné výhry typu  ?
?
Offline
#2 26. 01. 2016 19:40
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: hra s mincí
↑ Stýv:
Ahoj, n je pevné a nebo libovolné? Tj. musíme dosáhnout určitého daného n, abychom získali výhru, a nebo si ji můžeme vyplatit "kdykoli" (po několika pannách, jejichž počet označme n)?
"Máte úhel beta." "No to nemám."
Offline
#5 27. 01. 2016 17:51
Re: hra s mincí
↑ Xellos: éééé....? nejsem si jistý (jelikož jsi nenapsal, jak jsi dostal ten rekurentní vzorec, ani nějaký výseldek, který bych mohl zkontrolovat), ale mám dojem, že možná řešíš trochu jinou otázku, něž jsem měl na mysli. tak jen pro ujasnění:
neptám se na průměrný počet hodů do první výhry, ale na průměrný počet hodů potřebný k získání jedné výhry, tj. pokud je odpověď x, pak např. ve 100*x hodech očekávám, že vyhraju stokrát. možná je to to samé, ale nevím, nezkoumal jsem to
Offline
#6 27. 01. 2016 18:28
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: hra s mincí
↑ Stýv:
Asi tomu nerozumím. Jaká je strategie při hraní? Píšeš, že si můžeme vzít výhru, nebo můžeme pokračovat. Ale nepíšeš, jak se kdy rozhodneme. Na tom přece závisí výsledek. Pokud moje strategie bude "beru výhru vždy, když je za sebou 10-krát panna, jinak neberu" nebo "beru výhru vždy už při první panně", tak určitě dostanu různé výsledky.
Offline
#7 27. 01. 2016 18:35
#8 27. 01. 2016 18:43
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: hra s mincí
↑ Stýv:
Je v tom rozdíl, řekl bych: Pokud je n konkrétní pevné číslo (dané na počátku hry), řekněme 5, tak nemůžu přijmout výhru, pokud padnou třeba 4 panny. Naopak, pokud je n porměnné - a jen označuje počet padnouvších pannen, tak i když padnou 3, 5, apod. panny, tak vždy mohu přijmout výhru - a´t padne počet pannen po sobě jakýkoliv.
Jak to tedy je?
"Máte úhel beta." "No to nemám."
Offline
#9 27. 01. 2016 18:54
Re: hra s mincí
↑ check_drummer: ale výhru typu  můžeš zvolit jenom, pokud těch panen bylo
můžeš zvolit jenom, pokud těch panen bylo  . to
. to  může být libovolné, je to parametr v té úloze
může být libovolné, je to parametr v té úloze
Offline
#10 27. 01. 2016 19:47
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: hra s mincí
↑ Stýv:
Takže je to myšleno tak, že n je dané a ta hra se dá formulovat pro konkrétní n? Takže kdybych to formuloval třeba pro n=5, tak by ta úloha měla smysl? A ty chceš, abychom ji vyřešili pro každé n, je to tak? Stejně mi to nedává smysl. To by pak nemělo smysl mluvit o "výhře typu 5", protože by pro danou hru výhra jiného typu než 5 nebyla. Nebo můžou být různé (a tedy i lepší) výhry stejného typu? Pořád mi to zadání nedává smysl...
Offline
#11 27. 01. 2016 19:55
Re: hra s mincí
↑ Pavel Brožek: jo, asi se tím to zadání zbytečně "zkomplikovalo", holt je to slovní úloha ze života a ne zadání standardní rovnice pro průměrného žáčka SŠ. tak já tedy to přeformuluju:
Kdykoliv nám padne  -krát za sebou panna, vyhráváme (a začínáme počítat zase od 0). Když nám ovšem padne orel, tak se série pannen přeruší aniž bysme cokoliv získali (ale házíme dál).
-krát za sebou panna, vyhráváme (a začínáme počítat zase od 0). Když nám ovšem padne orel, tak se série pannen přeruší aniž bysme cokoliv získali (ale házíme dál).
Otázka zní: Kolik je průměrně potřeba hodů k získání jedné výhry (v závislosti na parametru  )?
)?
Offline
#12 27. 01. 2016 20:04
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: hra s mincí
↑ Stýv:
V tom případě ale nechápu, jaký je rozdíl mezi touhle úlohou a úlohou "kolik je průměrně potřeba hodů, abychom dosáhli toho, že n-krát za sebou padne panna". Pokud hru hraju a znám n a snažím se získat výhru, tak ji přece vezmu hned jak můžu. Pokud n neznám, pak ale musím mít nějakou strategii kdy výhru brát a kdy ne.
Pokud je to úloha ze života, tak ji spíš zkus formulovat pomocí pojmů ze života, třeba nám bude jasnější, jak to vlastně myslíš.
Offline
#14 27. 01. 2016 20:20
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: hra s mincí
No nevadí, jen se to pak dá formulovat jednodušeji a přijde mi to v rozporu s tím, že jsi psal:
Stýv napsal(a):
neptám se na průměrný počet hodů do první výhry
Offline
#15 27. 01. 2016 20:21
Re: hra s mincí
↑ Pavel Brožek: taky jsem ale psal "možná je to to samé, ale nevím, nezkoumal jsem to"
Offline
#16 27. 01. 2016 23:26
Re: hra s mincí
Tak ja som prave riesil priemerny pocet hodov na to, aby  -krat za sebou padla panna - ak prave padla
-krat za sebou padla panna - ak prave padla 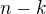 -krat za sebou. Spravim jeden hod. S pravdepodobnostou
-krat za sebou. Spravim jeden hod. S pravdepodobnostou  padne panna (teda je to od dalsieho hodu situacia s o 1 mensim
padne panna (teda je to od dalsieho hodu situacia s o 1 mensim  ), s rovnakou pravdepodobnostou orol (teda situacia s
), s rovnakou pravdepodobnostou orol (teda situacia s  ). Tot vse.
). Tot vse.
Offline
#18 28. 01. 2016 17:56
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: hra s mincí
↑ Xellos:
Ahoj, použil jsem podobný postup, resp. jednodušší
"Máte úhel beta." "No to nemám."
Offline
#19 30. 01. 2016 15:19
Re: hra s mincí
pro zajímavost přidám svoje řešení:
Offline
#20 30. 01. 2016 23:53
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: hra s mincí
Ahoj,
tomu nerozumím - mohl bys to prosím objasnit? - To platí vždy a nebo jen pro náš konkrétní problém?
"Máte úhel beta." "No to nemám."
Offline
#21 31. 01. 2016 00:04
Re: hra s mincí
↑ check_drummer: to jenom říkám, že střední hodnota alternativního rozdělení s parametrem p je p, to platí vždy
Offline
#22 31. 01. 2016 02:36
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: hra s mincí
↑ Stýv:
Ale ten očekávaný počet výher na jeden hod přece závisí na hitorii - na tom co padlo před tím hodem, který zkoumám...
"Máte úhel beta." "No to nemám."
Offline
#23 31. 01. 2016 10:19
Re: hra s mincí
↑ check_drummer: nepodmíněná střední hodnota na ničem nezávisí, to je prostě číslo
Offline
#24 31. 01. 2016 14:18
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: hra s mincí
↑ Stýv:
Ale pravděpodobnost p výhry v jednom hodu závisí na historii... Ta pravděpodobnost je totiž obecně jiná, jedná-li se o první hod a nebo o miliontý hod - např. je- n>1, tak prvním hodem nevyhraješ nikdy, kdežto miliontým vyhrát můžeš.
"Máte úhel beta." "No to nemám."
Offline

 poctu hodov ak treba na vyhru este
poctu hodov ak treba na vyhru este  )
) ako konstantu
ako konstantu  , vyriesit ez lin. rekurenciu a dosadenim za
, vyriesit ez lin. rekurenciu a dosadenim za  explicitne.
explicitne. .
. . Korektní ověření sem nepíšu, ale myšlenka je zhruba taková,že poté, co padne n-1 pan, tak buď padne ještě jedna - a máme co jsme chtěli - a nebo ne - a musíme začít "znova".
. Korektní ověření sem nepíšu, ale myšlenka je zhruba taková,že poté, co padne n-1 pan, tak buď padne ještě jedna - a máme co jsme chtěli - a nebo ne - a musíme začít "znova". - a pokud vyjádříme z tohoto vztahu (rekurentně) E(n-1) a tak postupujeme iterativně dál, tak dostaneme
- a pokud vyjádříme z tohoto vztahu (rekurentně) E(n-1) a tak postupujeme iterativně dál, tak dostaneme 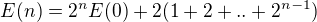 a protože je E(0)=0, tak součtem té geometrické řady máme
a protože je E(0)=0, tak součtem té geometrické řady máme 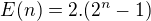 .
. výhry v jednom hodu. při hodu vyhraju, pokud mi padne panna a pokud současně předtím padla série právě
výhry v jednom hodu. při hodu vyhraju, pokud mi padne panna a pokud současně předtím padla série právě  pannen (a před ní orel) pro nějaké
pannen (a před ní orel) pro nějaké 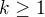 , odtud
, odtud  a řešením je tedy
a řešením je tedy 