Matematické Fórum

marketa0007777 · 27. 01. 2016 23:13

Zdravím, potřebovala bych pomoct s řešením této úlohy.
Pomocí druhé derivace funkce $t^{2}/t-4$ najděte inflexní body a určete intervaly konvexnosti a konkávnosti.

Druhou derivací mám, ale nevím co dál, děkuji za rady...

runcorne · 27. 01. 2016 23:45

↑ marketa0007777:

Zdravím,

je nutno spočítat, pro která t se druhá derivace rovná nule. Tyto body mohou být inflexní. Potvrdit to lze tak, že zjistíme, na kterých intervalech je funkce konvexní (druhá derivace větší než nula) a konkávní (menší než nula). Pokud se v daném bodě (který je součástí Df) mění znaménko druhé derivace, pak je tento bod inflexní.

marketa0007777 · 27. 01. 2016 23:50

↑ runcorne: je možné, že mi vychází diskriminant pri zjisštění inflexních bodů 80?

Al1 · 28. 01. 2016 10:05

↑ marketa0007777:

Zdravím,

mně vyšla druhá derivace $y=\frac{t^{2}}{t-4}$ jako $y^{\prime\prime}=\frac{32}{(t-4)^{3}}$

Rumburak

↑ marketa0007777:

Ahoj.

Začal vych určením definičního oboru. Je jím sjednocení intervalů $(-\infty, 4) , (4, \infty)$ .
Konvexnost resp. konkávnost musíme řešit na každém z těchto intervalů zvlášť.

Předpis pro funkci bych ještě poněkud upravil, aby se s ní pohodlněji pracovalo:

$y=\frac{t^{2}}{t-4} = \frac{t^{2} - 16}{t-4} + \frac{16}{t-4} = t+4 + \frac{16}{t-4}$ .

Nejsem zastáncem pouze technických návodů typu "udělej to a to" bez dalšího vysvěltení a zdůvodnění.
Že nekonstantní hladká funkce je na intervalu konvexní, intuitivně znamená, že se nikde v tomto intervalu
"nezpomaluje" její případný růst ani "nezrychluje" její případné klesání.
Obdobným způsobem lze objastnit, co znamená, když je funkce na intervalu konkávní.
Odtud plyne metoda zjišťování kovexnost resp. konkávnosti funkce vyšetřováním průběhu její derivace.
Inflexní bod je takový, jehož průchodem se kovexnost funkce změní na konkávnost nebo naopak.

marketa0007777 · 28. 01. 2016 13:15

↑ Rumburak: takže s derivací vůbec nemusím pracovat? Mám ji v zadání, tak se bojím, aby to nebyla chyba..... jinak druhá derivace mi vyšla $t^{2}-4t-16/ (t^{2}-16)^{2}$

Rumburak

↑ marketa0007777:

Netvrdím, že s derivací není třeba pracovat, nicméně je dpbré vědět, proč s ní pracujeme právě tak a tak.
Znaménko první derivace funkce $f$ nám říká, zda je funkce $f$ v daném intervalu rostoucí nebo klesající ,
absolutní hodnota první derivace charakterisuje míru ("rychlost") toho růstu resp. klesání v určitém bodě.
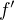Druhá derivace funkce $f$ pak obdobným způsobem vypovídá o vlastnostech funkce $f'$ . Chceme-li tedy
nalézt interval, na němž je funkce $f$ (majícÍ druhou derivaci) konvexní, hledáme interval, na němž je
funkce 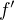$f'$ neklesající, tedy interval, kde platí $f''(x) \ge 0$ .

Úpravu $y = t + 4 + \frac{16}{t-4} = t + 4 + 16(t-4)^{-1}$ jsem provedl proto, aby se snadno
derivovalo:

$y' = 1 + 16(-1)(t-4)^{-2}$ , $y'' = 16(-1)(-2)(t-4)^{-3}$

atd.

marketa0007777 · 28. 01. 2016 14:19

↑ Rumburak: a muj výsledek derivace je správný?

misaH · 28. 01. 2016 14:27 — Editoval misaH (28. 01. 2016 14:31)

$y^{\prime\prime}=\frac{32}{(t-4)^{3}}$

(Prevzaté z príspevku od Al1 - :-) zdravím.)

Ak ju máš takto, tak áno.

Rumburak ju má rovnakú, len ináč zapísanú.

Tá tvoja je zrejme zle, stačí porovnať.

Matematické Fórum

#1 27. 01. 2016 23:13

inflexní body

#2 27. 01. 2016 23:45

Re: inflexní body

#3 27. 01. 2016 23:50

Re: inflexní body

#4 28. 01. 2016 10:05

Re: inflexní body

#5 28. 01. 2016 11:16 — Editoval Rumburak (28. 01. 2016 13:29)

Re: inflexní body

#6 28. 01. 2016 13:15

Re: inflexní body

#7 28. 01. 2016 13:53 — Editoval Rumburak (28. 01. 2016 13:56)

Re: inflexní body

#8 28. 01. 2016 14:19

Re: inflexní body

#9 28. 01. 2016 14:27 — Editoval misaH (28. 01. 2016 14:31)

Re: inflexní body

Zápatí