Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 02. 2016 13:10
- Contemplator

- Příspěvky: 362
- Reputace: 0
Integrál - príklad
Dobrý deň, mám integrál: 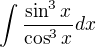 a cez subst. a parcialne zlomky som sa dostal k tomuto:
a cez subst. a parcialne zlomky som sa dostal k tomuto: a neviem ako to zintegrovať. Môžte mi niekto poradiť? :) na
a neviem ako to zintegrovať. Môžte mi niekto poradiť? :) na 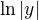 ani
ani 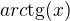 ani arc\sin (x) to neviem upraviť
ani arc\sin (x) to neviem upraviť
Offline
#2 03. 02. 2016 13:31
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Integrál - príklad
↑ Contemplator:
Mě po substituci t= sin x a porozkladu na parciální zlomky vychází:
Nikdo není dokonalý
Offline
#4 03. 02. 2016 15:32
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Integrál - príklad
↑ Cheop: ano takto to vyšlo aj mne, akurát že ten posledný int. mám 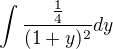 a neviem ako to zintegrovať....
a neviem ako to zintegrovať....
↑ Rumburak: Očividne je to ovela jednoduchšie :) - ďakujem, ale nerozumiem tomuto: "Nutno správně určit intervaly, na nichž má nalezená primiivní funkce platnost."
Offline
#5 03. 02. 2016 15:39 Příspěvek uživatele Contemplator byl skryt uživatelem Contemplator. Důvod: skrat...
#6 03. 02. 2016 15:54 — Editoval Rumburak (03. 02. 2016 15:55)
Re: Integrál - príklad
↑ Contemplator:
Primitivní funkce je vždy svázáná s nějakým intervalem, který bychom měli uvést, když o PF hovoříme.
Např. 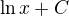 je PF k
je PF k  na
na  , zatímco
, zatímco 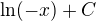 je PF k
je PF k  na
na 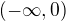 .
.
V tabulkách se často uvádí, že PF k  je
je  pro
pro  , ale není to přesné . PF k
, ale není to přesné . PF k 
nutno vnímat jako spojitou funkci na intervalu, která v každém jeho bodě  má derivací
má derivací  .
.
Offline
#7 03. 02. 2016 19:09
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Integrál - príklad
↑ Rumburak: mmmh, už tomu rozumiem. Podla teba : to vychádza:
to vychádza: a keď som to počítal cez toto:
a keď som to počítal cez toto: 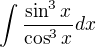 subst:
subst: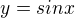 =
= 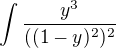 tak mi vychádza:
tak mi vychádza:  čo sa po dosadení hodnot nerovná..... škoda že to nemožem odfotit a hodiť to sem, alebo je tu nejaký konvertér na to? (fotka je moc velká)
čo sa po dosadení hodnot nerovná..... škoda že to nemožem odfotit a hodiť to sem, alebo je tu nejaký konvertér na to? (fotka je moc velká)
Offline
#8 05. 02. 2016 09:50 — Editoval Rumburak (05. 02. 2016 09:51)
Re: Integrál - príklad
↑ Contemplator:
V případě úlohy na zjištění PF se dá výsledek zkontrolovat zderivováním nalezené funkce.
Pro substuci  je přechod k
je přechod k  chybný, správně mělo vyjít
chybný, správně mělo vyjít
 .
.
Offline
#9 06. 02. 2016 22:50
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Integrál - príklad
↑ Rumburak: a Jak je možné, že to s tou subst. nevychádza? ty si to overil len pomocou toho kroku kde sa to ešte len chystá na rozklad na parc. zlomky, že to nevychádza? - tak z toho potom vyplýva, že tou subst. to nemôžem riešiť ? nerozumiem a je to zaujímave... :D
Offline
#10 06. 02. 2016 23:39 — Editoval Al1 (06. 02. 2016 23:43)
Re: Integrál - príklad
↑ Contemplator:
Zdravím,
při užití substituce 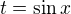 a rozkladu na parciální zlomky
a rozkladu na parciální zlomky 
dostaneš 
a po resubstituci
A zbytek je na úpravě
Offline
#11 07. 02. 2016 14:43
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Integrál - príklad
↑ Rumburak: mne to ale cez tú subst. vyšlo 
↑ Al1: Niečo mi tam nesedí: Mne vyšli A,B,C,D v parc. zlomokch: -1/2 , 1/4 , 1/2 , -1/4 a potom ďalej: a to je iné o znamienko a potom som to ale ešte integroval tak že tam kde sú tie druhé mocniny - som to zderivoval a upravil na:
a to je iné o znamienko a potom som to ale ešte integroval tak že tam kde sú tie druhé mocniny - som to zderivoval a upravil na: 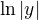 môžem to urobiť vôbec?
môžem to urobiť vôbec?
Offline
#12 07. 02. 2016 15:46
#13 07. 02. 2016 16:28
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Integrál - príklad
↑ Al1: Takže to môžem zintegrovať iba takto? nemôžem spraviť toto?: 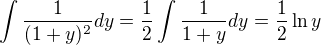
Offline
#14 07. 02. 2016 16:37
Re: Integrál - príklad
↑ Contemplator:
To rozhodně ne, jakým způsobem jsi uvažoval? Vždyť zpětně derivuj 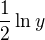 , dostaneš
, dostaneš  a kde je
a kde je  ?
?
Offline
#15 07. 02. 2016 17:33 — Editoval Contemplator (07. 02. 2016 17:35)
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Integrál - príklad
↑ Al1: tak potom je niečo zle uložené v mojom mozgu , z tohto som vychádzal 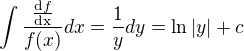 , subst:
, subst: 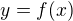 $,
$,
Offline
#17 07. 02. 2016 17:53
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Integrál - príklad
↑ Al1:Ahá , už viem kde som skratoval.... ďakujem :)
Offline
#18 07. 02. 2016 18:24
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Integrál - príklad
Aj tak mi ale vyšli :
 a to je iné než tvoje ↑ Al1: takže tebe asi vyšlo B =-1/4 a D=1/4 čo je opačné ako to vyšlo mne ...
a to je iné než tvoje ↑ Al1: takže tebe asi vyšlo B =-1/4 a D=1/4 čo je opačné ako to vyšlo mne ...
Offline
#19 07. 02. 2016 20:33 — Editoval Al1 (07. 02. 2016 20:38)
Re: Integrál - príklad
↑ Contemplator:
Mně ta znaménka vyšla úplně stejně ( mám jen proměnnou t)
Edit: už vidím tvou chybu v uvažování, ono totiž platí:
Offline
#20 07. 02. 2016 22:34
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Integrál - príklad
↑ Al1: No, to je dosť dobré, že si to uvidel:) ďakujem, ale prečo potom keď si zoberem toto  výjmem mínus, a vyhodím ho pred integrál a mám :
výjmem mínus, a vyhodím ho pred integrál a mám :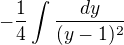 a to nie je to isté ako:
a to nie je to isté ako: 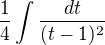
Offline
#21 07. 02. 2016 22:53 — Editoval Al1 (07. 02. 2016 23:04)
Re: Integrál - príklad
↑ Contemplator:
Tvůj zápis z příspěvku #11
Shodli jsme se na tom, že  , takže
, takže 
Já mám rozklad na parciální zlomky
Po přeskupení mi vychází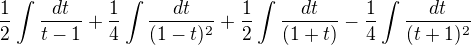 , což je stejné jako
, což je stejné jako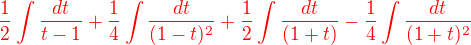
Kontrola Odkaz
Offline
#22 08. 02. 2016 12:07 — Editoval Contemplator (08. 02. 2016 12:08)
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Integrál - príklad
↑ Al1: Áno, vidím, že mám rovnaký výsledok ale, to čo som sa pýtal v minulom príspevku som z toho čo si mi odpísal nepochopil, pretože keď mám  výjmem mínus, a vyhodím ho pred integrál, tak mám :
výjmem mínus, a vyhodím ho pred integrál, tak mám :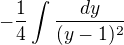 a tam je :
a tam je :  a potom by som mal tie parc. zlomky: 1/2.... ,
a potom by som mal tie parc. zlomky: 1/2.... , 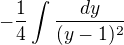 , 1/2....... ,
, 1/2....... , 
Offline
#23 08. 02. 2016 12:16 — Editoval Rumburak (08. 02. 2016 12:17)
Re: Integrál - príklad
↑ Contemplator:
Ahoj.
Ve jmenovateli zlomku 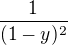 je sudá mocnina, takže
je sudá mocnina, takže  ,
,
tudíž ono vytýkání (-1) je zde chybou.
Offline
#24 08. 02. 2016 12:39
- Contemplator

- Příspěvky: 362
- Reputace: 0
Re: Integrál - príklad
↑ Rumburak: AHHHHHHHHHHHHHÁ , takže ono to je chyba a tamtú rovnosť som si musel uvedomiť, aby som to pochopil. A prečo je to chyba? Prečo nemôžem vyjmuť - keď je párna mocnina , takže keď je nepárna, tak môžem ?
Offline

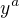 .
.
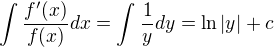
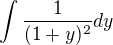 a derivace jmenovatele je
a derivace jmenovatele je  a to do čitatele těžko dostaneš
a to do čitatele těžko dostaneš