Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 09. 02. 2016 18:51

Contemplator
Příspěvky: 362
Reputace:   0 
 

priebeh funckie s absolútnou hodnotou

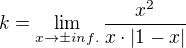Dobrý podvečer prajem, chcem sa spýtať ako získať asymptoty so smernicou  pri takto zadanom príklade: $\frac{x^{2}}{|1-x|}$   takto zapíšem: $k=\lim_{x\to \pm inf.}\frac{x^{2}}{x\cdot |1-x|}$ no a čo teraz každu tú limitu do +-inf rozpoliť na 2 prípady kvôoli abs. hodnote alebo ako?

Tak isto by som rád vedel či pri deriváciach   rozlíšiť tie 2 prípady pre x>1 a pre x<1

Offline

 

#2 09. 02. 2016 20:02

vanok
Příspěvky: 14606
Reputace:   742 
 

Re: priebeh funckie s absolútnou hodnotou

Ahoj ↑ Contemplator:,
Vsak ti ide o vysetrenie limit v okoli + a - infini. Tak uprav Tvoj vyraz na kazdu situaciu .
Ake limity budes tak hladat?

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#3 09. 02. 2016 21:25

Contemplator
Příspěvky: 362
Reputace:   0 
 

Re: priebeh funckie s absolútnou hodnotou

kazdu zo štyroch, alebo z dvoch?

Offline

 

#4 09. 02. 2016 21:34

Freedy
Místo: Praha
Příspěvky: 2726
Škola: MFF UK (15-18, Bc.)
Pozice: student
Reputace:   166 
 

Re: priebeh funckie s absolútnou hodnotou

↑ Contemplator:
jak lze přepsat absolutní hodnotu $|1-x|$, když je $x>1$ (když jde do nekonečna), popřípadě když $x<1$ (když jde do -nekonečna)?

L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho

Offline

 

#5 09. 02. 2016 22:08

Contemplator
Příspěvky: 362
Reputace:   0 
 

Re: priebeh funckie s absolútnou hodnotou

↑ Freedy: 1-x    ak $x>1$ a  x-1 ak$x<1$

Offline

 

#6 09. 02. 2016 22:28

Al1
Příspěvky: 7797
Reputace:   542 
 

Re: priebeh funckie s absolútnou hodnotou

↑ Contemplator:

Zdravím,
odstraňuješ $|1-x|$
Potom pro

$1-x<0\nl x>1\Rightarrow |1-x|=-(1-x)=x-1$
a pro
$1-x>0\nl x<1\Rightarrow |1-x|=1-x $

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson