Matematické Fórum

byk7 · 09. 02. 2016 16:24

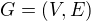Označme $H[X]$ podgraf souvislého (neorientovaného, jednoduchého) grafu $G=(V,E)$ indukovaný množinou 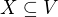$X\subseteq V$ . Dokažte, že existuje neprázdná podmnožina vrcholů $X$ splňující $|E(H[X])|+|E(H[V\setminus X])|<\frac12|E(G)|$ .

check_drummer · 10. 02. 2016 18:50

↑ byk7:
Ahoj, co zkusit pravděpodobnostní postup? Volit X náhdoně a spočítat střední hodnotu (nebo její odhad) pro ten součet na levé straně. Případně uvažovat jen ty G, pro které nelze X nalézt triviálně.

byk7 · 10. 02. 2016 19:07

↑ check_drummer:

Díky, vyzkouším, až budu mít čas. Nicméně ta úloha by měla být řešitelná nějakým elementárním postupem, který mi uniká.

check_drummer · 10. 02. 2016 21:45

↑ byk7:
Co zkusit maximální párování a vrcholy na koncích hran toho párování definovat množinu X (resp. V\X)?

byk7 · 13. 02. 2016 19:47

Tak prý indukce. Nerovnost si upravíme do tvaru $|E(H[X])|+|E(H[V\setminus X])|<|E(G)|-|E(H[X])|-|E(H[V\setminus X])|$
(na pravé straně tak dostáváme hrany vedoucí pouze mezi podgrafy $H[X]$ a $H[V\setminus X]$ ).

1) Nechť je 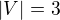$|V|=3$ , možnosti jsou jen dvě: cesta 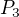$P_3$ a cyklus 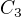$C_3$ , existence množiny $X$ je pak zřejmá.
2) Nechť je $G$ graf vyhovující zadání a 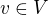$v\in V$ . Z indukčního předpokladu umíme graf 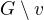$G\setminus v$ rozdělit. Vrchol $v$ pak dáme do množiny, kde mám méně sousedů. Pokud jich má v obou stejně, pak ho umístíme libovolně.