Matematické Fórum

Freedy · 08. 02. 2016 23:03 — Editoval Freedy (08. 02. 2016 23:04)

Ahoj,

chtěl bych se jen zeptat, zda-li někdo nemá nápad, jak by se dala řešit tato úloha:

Určete, pro která $c\in \mathbb{R}$
$\frac{|x+1|^{\frac{3}{2}}}{x^{\frac{1}{3}}}=c$
a) alespoň 2 řešení
b) právě jedno řešení

nicméně bez použití průběhu funkce.
Ten je u tohoto příkladu celkem jednoduchý (jedná se o příklad ze zkouškové písemky).
Zkoušel jsem to nějak mocnit, odstraňovat abs. h, nicméně to k ničemu nevede.

Nehledám x vyjádřené pomocí c, stačí jenom ukázat, pro která c to má 2 řešení / právě 1.

Děkuji ;)
Freedy

byk7 · 09. 02. 2016 00:25 — Editoval byk7 (09. 02. 2016 03:40)

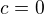Označme $f(x):=\frac{|x+1|^{\frac{3}{2}}}{x^{\frac{1}{3}}}$ a předpokládejme $x<0$ . Zřejmě $f(-1)=0$ a pro $x\neq-1$ je $f(x)<0$ (tzn. pro $c=0$ dostáváme jedno řešení). Čitatel i jmenovatel jsou na 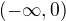$(-\infty,0)$ spojité funkce, tedy i $f$ je na tomto intervalu spojitá. Dále je zřejmé, že $x\to0^-\Rightarrow f(x)\to-\infty$ . Pro dostatečně malá $x$ je
$|x+1|^{3/2}\ge\left|\frac{x}{2}\right|^{3/2}\Rightarrow f(x)\le\frac{1}{2\sqrt{2}}\frac{|x|^{3/2}}{x^{1/3}}=\frac{1}{2\sqrt2}\frac{|x|^{3/2}}{\sqrt[3]{\mathrm{sgn}(x)}\cdot|x|^{1/3}}=-\frac{1}{2\sqrt2}\cdot|x|^{7/6}\to-\infty$
a tedy i $f(x)\to-\infty$ (pro $x\to-\infty$ ).

To nám dohromady dává (spojitost, ne-/ohraničenost zdola/shora), že pro $c<0$ má rovnice $f(x)=c$ alespoň dvě řešení.

Případ $x>0$ ještě rozmyslím.

Edit.:
Podle AG nerovnosti platí
$\frac{7x+7x+2+2+2+2+2+2+2}{9}\ge\sqrt[9]{2^7(7x)^2}$ s rovností nastávající pro $x=2/7$ , po umocnění na devátou
$$\frac{14}{9}$^9(x+1)^9\ge2^7 7^2 x^2$ , odtud
$(x+1)^9\ge\frac{9^9}{2^7 7^2} x^2\ \Rightarrow\ \alpha:=\frac{27}{2\sqrt[6]{2}\sqrt[3]{7}}\le f(x)$
a opět z $$x\to0^+\vee x\to\infty$\ \Rightarrow\ f(x)\to\infty$ a spojitosti máme, že, pro $c=\alpha$ má rovnice $f(x)=c$ jedno řešení a pro $c>\alpha$ má alespoň dvě řešení.

Závěr:
Rovnice $f(x)=c$ má:
a) alespoň dvě řešení pro $c<0\vee c>\alpha$ ,
b) právě jedno řešení pro $c=0\vee c=\alpha$ .

jelena · 09. 02. 2016 20:45

Zdravím,

↑ Freedy: přečetla jsem reputaci kolegy Ondry - takový efektní zápis a není vyřešeno? :-)

Jak se myslí, že bez "průběhu funkce", mohu rozebírat jednotlivé funkce v podílu jen na základě SŠ? Nesmím použit diferenciální počet, nebo co se nesmí? Děkuji.

Freedy · 09. 02. 2016 20:51

↑ jelena:
ahoj,

já jsem s Ondrou řešil tady ten příklad na fb, nicméně jsem mu vysvětlil, že v podstatě použil to, co já jsem nechtěl.

Nechci používat limity apodobně. Zajímalo by mě, stejně jako se například při určování počtu kořenů kvadratické rovnice zkoumá diskriminant, zda-li by se něco podobného nedalo udělat zde.

Samozřejmě trik s AG-nerovností celkem oceňuji. Je to opravdu brilantní nápad, nicméně se zde pořád využívá dif. počet.
Nemyslím ani tak SŠ matematiku, klidně i vysokoškolskou, nicméně ne-analytickou metodu.
Na tuto otázku jsem se ptal, protože v algebře a podobných disciplínách rozhodně nemám takový nadhled jako špička tohoto fóra, takže mě zajímaly názory ostatních.
Uvidíme, zda-li se ještě někdo ozve
↑ jelena:
vy nějaký nápad máte? :)

jelena · 09. 02. 2016 21:47

↑ Freedy:

děkuji, na fb stále nemám účet (ale už jsem si zvykla, že se tam musí hledat aktuální informace, např. u nás používá divadlo, nebo když potřebuji si zjistit novinky v opavském stravování apod.) :-)

my máme nápad, že mohu bez použití dif. počtu rozebrat funkci $\frac{|x+1|^{9}}{x^2}$ (podíl snadno popsatelných funkcí, speciální zaměření na minimální hodnotu čitatele a vždy kladný jmenovatel, k tomu chování na intervalech, kde základy mocnin jsou v intervalech od 0 do 1 - tak schematicky bych popsala). Tímto jsem však ovlivnila, že pravá strana (c, které mohlo být i záporné) po umocnění ^6 se promění na jen kladné hodnoty. Asi budu donucena pracovat s rozkladem na součin.

Uvidíme, zda-li se ještě někdo ozve

:-) Také se za to přimlouvám, přesunu do zajímavých pro SŠ.

byk7 · 09. 02. 2016 23:00

↑ jelena:

To se dá opravit, prvně rozebereme případ 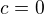$c=0$ , který není náročný. Následně si všimneme, že $x\neq-1$ a $c$ musí mít nutně stejné znaménko, takže rovnici $|x+1|^{3/2}=c\cdot x^{1/3}$ můžeme bez obav umocnit, protože obě strany jsou kladné, tzn. máme rovnici $|x+1|^9=c^6\cdot x^2$ .

Předpokládejme, že $c,x>0$ , tzn. $(x+1)^9=c^6\cdot x^2$ (1), zafixujme levou stranu a na pravou stranu se dívejme jako na parabolu s proměnným vedoucím koeficientem. Z geometrického názoru je zřejmé, že existuje konstanta $\alpha$ taková, že pro $c<\alpha$ nemá rovnice (1) řešení (polynom $(x+1)^9$ parabole uteče příliš brzo) a pro $c>\alpha$ má rovnice právě dvě řešení (polynom $(x+1)^9$ se nijak nevlní a jinak se chová dobře (má pouze jeden kořen)). Při volbě $c=\alpha$ dojde pouze k dotyku a $\alpha$ určíme pomocí AG (viz výše). Odtud taky můžeme odhadnout, že pro $c>\alpha$ bude jeden kořen v intervalu $(0,\tfrac27)$ a druhý v $(\tfrac27,\infty)$ .

Nechť je nyní $c,x<0$ . Tento případ je jednodušší – funkce $|x+1|^9$ roste na intervalu $[-1,0]$ a $c^6\cdot x^2$ tu klesá, ze spojitosti a nezápornosti obou funkcí na tomto intervalu plyne, že tu mají společný právě jeden bod. Pro $x<-1$ je pak zřejmé, že pro $x\to-\infty$ roste polynom $-(x+1)^9$ do nekonečna rychleji než parabola.

Závěr je stejný jako v původním příspěvku. Tady jsem používal spíše naivní geometrické představy, což dává středoškolštější řešení (ovšem za cenu méně pevných základů).

Pokud jedeme s x od -1 do -oo, tzn. zprava, pak skutečně funkční hodnoty obou funkcí rostou, ačkoliv jsou obě funkce na (-oo,-1] klesající (při běžném pohledu / zleva směrem doprava).

jelena · 10. 02. 2016 20:49

↑ byk7:

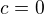děkuji, také využívám geometrické představy, ve všem je to cca shodné (a podílem se mi vyhodnocovalo sice o něco přehledněji, ale i přepis na tvar $(x+1)^9=c^6\cdot x^2$ jsem také musela použit). Bohužel ale nemám předpoklady na nalezení hodnoty $c$ (mimo $c=0$ ), už bych musela používat derivace, jelikož bych musela pracovat s tečnou (alespoň v mém odhadu).

ještě se odměním za odvahu psát do zajímavých :-) A zdravím.

-------------------------

Mohu se zeptat, proč v názvu tohoto příspěvku stojí vyrazy rovnice a nerovnice? Máme chápat toto téma jako uzavřené, nebo příjdou ještě další úlohy, třeba (jak by název napovídal) úpravy algebraických výrazů nebo řešení nerovnic? (c)

Freedy · 11. 02. 2016 14:41 — Editoval Freedy (11. 02. 2016 14:42)

jelena napsal(a):
děkuji, na fb stále nemám účet

;) naprosto to chápu... Já beru naopak fb jako nástroj pro komunikaci. Až v druhé řadě je to nějaký zdroj informací a podobně, nicméně ani tam to matematicky nechátrá, nicméně jako náhrada za podobná fóra jako je toto, se to považovat nedá. Tam se bohužel ozývá moc "matematicky nenadaných" lidí...

jinak nápady máte dobré, obzvlášť ↑ byk7: bych doporučil, že i spánek je někdo vhodný víc, než přemýšlení nad parabolama :D

-------------------------
Nevím, v podstatě jsem myslel, že myšlenka se bude ubírat tímto směrem, nicméně příspěvky vás obou nabídly jiné "nediferenciální" řešení...
Lze akorát spekulovat nad tím, zda-li se zkoumání paraboly goemetricky nepovažuje za průběh...
Při zjišťování počtu kořenů kvadratické rovnice se v podstatě také koukáme geometricky, protože na začátku vycházíme z paraboly -.-

jelena · 13. 02. 2016 00:45

↑ Freedy:

:-) já jsem přes den tak vykomunikována, že již další nehledám. Ale informace ano - patrně pro snadnou údržbu, použití a nizkonákladovost fb využívají různé zájmové spolky.

Lze akorát spekulovat nad tím, zda-li se zkoumání paraboly goemetricky nepovažuje za průběh...

pokud si vybavuji, tak se odděluji užití vlastností elementárních funkcí vč. funkcí vzniklých z elementárních pomocí operací a složených funkcí od vyšetření průběhu funkce užitím dif. počtu. V praktickém použití asi nějaká hranice není, jen pokud přímo zadáním není omezení použitých metod.

K úloze - ještě jsem uvažovala nad zavedením substituce 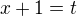$x+1=t$ , potom by vznikl polynom (po úpravě) $t^9=c^6\cdot (t-1)^2$ , zda by to nějak nešlo použit snadněji, využitím vlast. kořenů polynomů? (zatím jsem vynechala abs. hodnotu). Oficiální řešení je k dispozici? Děkuji.

spánek je někdo vhodný víc

:-) naprostý souhlas, dobrou noc (c).

Matematické Fórum

#1 08. 02. 2016 23:03 — Editoval Freedy (08. 02. 2016 23:04)

rovnice s parametrem

#2 09. 02. 2016 00:25 — Editoval byk7 (09. 02. 2016 03:40)

Re: rovnice s parametrem

#3 09. 02. 2016 00:40 Příspěvek uživatele vanok byl skryt uživatelem vanok. Důvod: Necham pomahat kolegu Byka sameho

#4 09. 02. 2016 20:45

Re: rovnice s parametrem

#5 09. 02. 2016 20:51

Re: rovnice s parametrem

#6 09. 02. 2016 21:47

Re: rovnice s parametrem

#7 09. 02. 2016 23:00

Re: rovnice s parametrem

#8 10. 02. 2016 20:49

Re: rovnice s parametrem

#9 11. 02. 2016 14:41 — Editoval Freedy (11. 02. 2016 14:42)

Re: rovnice s parametrem

jelena napsal(a):

#10 13. 02. 2016 00:45

Re: rovnice s parametrem

Zápatí