Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 16. 02. 2016 18:03 — Editoval vanok (16. 02. 2018 16:30)
Re: Determinant
↑ byk7:,
Ahoj,
Osobne som najprv hladal matice A, ktore vyhovuju danej rovnici.
Evidentne, pre kazde n, matica 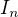 vyhovuje.
vyhovuje.
Potom mozme vysetrit problem pre kazde n. ( co som zatial nerobil)
Od tial sa potom lahko urci hladany determinant.
A ty si nasiel ake riesenie?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 15. 02. 2018 15:51 — Editoval vanok (26. 02. 2018 11:11)
Re: Determinant
Ahoj ↑ laszky:,
Napis podrobne tvoje riesenie. Dakujem.
Mala otazka. Co by si povedal o komplexnej matici radu 1 takej, ze 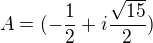 ?
?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 24. 02. 2018 11:02 — Editoval vanok (24. 02. 2018 11:04) Příspěvek uživatele vanok byl skryt uživatelem vanok. Důvod: Duplicifa
#6 08. 03. 2018 23:42
Re: Determinant
↑ vanok:
Sel jsem na to takto:
Pokud je 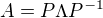 Jordanuv rozklad matice
Jordanuv rozklad matice  , potom
, potom 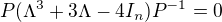 . Takze
. Takze  je podobna nulove matici a ma tedy vsechna vlastni cisla nulova. Protoze je M zaroven horni trojuhelnikova, ma na diagonale vlastni cisla, tj nuly. Vlastni cisla matice
je podobna nulove matici a ma tedy vsechna vlastni cisla nulova. Protoze je M zaroven horni trojuhelnikova, ma na diagonale vlastni cisla, tj nuly. Vlastni cisla matice 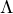 jsou tedy resenim rovnice
jsou tedy resenim rovnice  . Proto ma
. Proto ma 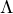 na diagonale bud jednicky, nebo pary komplexnich cisel
na diagonale bud jednicky, nebo pary komplexnich cisel 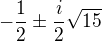 . Matice
. Matice 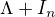 ma na diagonale bud dvojky, nebo pary komplexnich cisel
ma na diagonale bud dvojky, nebo pary komplexnich cisel 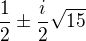 . Soucin tohoto paru komplexnich cisel je
. Soucin tohoto paru komplexnich cisel je  . Takze
. Takze  . Proto je i
. Proto je i  .
.
Vanok: Na tu komplexni matici ti nepovim nic. :-)
Offline
#7 09. 03. 2018 00:25 — Editoval vanok (24. 07. 2019 11:43)
Re: Determinant
Je jPozdravujem ↑ laszky:,
Ano pre realne matice je to jednoduche. ( pouzitim Cayley Hamilton)
Ale zatial nemam vseobecnu odpoved v inych situaciach. ( pre ine télesa)
No kolega ↑ byk7: neupresnil ci treba vysetrit aj take ine situacie.
Édit. Cf. Upresnenie
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 09. 03. 2018 00:44
Re: Determinant
Ano, ale tie ine situacie mozno su mozno o mnoho tazsie a zaujimavejsie ...
Mozno sa k tomu po case vratime.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 24. 07. 2019 12:09 — Editoval vanok (24. 07. 2019 12:11)
Re: Determinant
↑ vanok:,
Pridam este maly doplnok v pripade realnych matic.
Minimalny polynom matice A je vzdy delitelom [ ktoreho factory su  alebo aj suciny ich mocnin] charakteristickeho polynomu
alebo aj suciny ich mocnin] charakteristickeho polynomu  ( ktory je stupna n) tejto matice [ ktory je
( ktory je stupna n) tejto matice [ ktory je  ].
].
Tak mame 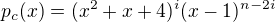 pre jedno cele i,
pre jedno cele i,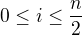 ,
,
to nam okamzite hladany determinant [ ktory je 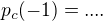 ]
]
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

 splňující
splňující 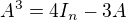 . Určete
. Určete  .
. .
. tak je jasne ze napr. polynome p taky ze
tak je jasne ze napr. polynome p taky ze 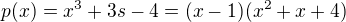 je anulovany maticou A jeho jedinny realny koren je x=1. Tak jeho minimalny polynom
je anulovany maticou A jeho jedinny realny koren je x=1. Tak jeho minimalny polynom 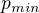 je taky ze
je taky ze 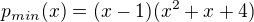
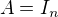 je co v tejto situacii vyhovuje.
je co v tejto situacii vyhovuje.