Matematické Fórum

FlyingMonkey · 16. 04. 2012 15:34

Ahoj,

"Určete stranu čtverce, které musíme vyříznout ve všech rozích obdélníkového papíru o rozměrech 8cm x 5cm tak, aby po složení vznikla krabička maximálního objemu ... "
tyhle příklady jsem zatím v podstatě vůbec nedělal, takže bych prosil o pomoc :)
Vím, že základní myšlenka bude, vyjádřit si závislost nějaké veličiny na jiné ... nebo nějak tak ^^

Tak V = a^3 a tím končím? :))
Jakože tu představu mám, myslím, docela přesnou ... Ale co s tím? Prosím o radu, díky )

rleg · 16. 04. 2012 15:50 — Editoval rleg (16. 04. 2012 15:53)

Ahoj
podle mě bys měl postupovat zhruba takto
Objem krabičky bude podstava krát výška. Obsah podstavy bude (8-2x).(5-2x) a výška=x, kde x je strana čtverce, který vyřežeme v každém rohu.

čili bych to zhruba viděl na $V=40x-26x^2+4x^3$ . Když tohle zderivuješ, najdeš extrémy a pak jen musíš najít maximum.

Samozřejmě je ta funkce řešitelná v intervalu (0;2,5)

Cheop · 16. 04. 2012 16:14 — Editoval Cheop (16. 04. 2012 16:15)

↑ FlyingMonkey:
Po zobecnění:
Máme-li obdélníko rozměrech $a$ a $b$ pak strana čverce (x), který musíme vyříznout v rozích je:
$x=\frac{a+b-\sqrt{a^2-ab+b^2}}{6}$ - tady bude objem maximální

jelinekgreen · 16. 04. 2012 16:47

↑ Cheop:
Jestli můžu poprosit o rozvedení (hlavně co se teorie týče) tohohle vzorce?

Cheop · 16. 04. 2012 21:27 — Editoval Cheop (16. 04. 2012 21:28)

↑ jelinekgreen:
Objem bude:
$V=x(a-2x)(b-2x)\,\Rightarrow\text{max}$ - úpravou:
$V=4x^3-2x^2(a+b)+abx\,\Rightarrow\,\text{max}$
Tuto funkci derivujeme podle x a derivaci položíme =0 tedy:
$V'=12x^2-4x(a+b)+ab=0\\x_{1,2}=\frac{4(a+b)\pm\sqrt{16(a+b)^2-48ab}}{24}\\x_{1,2}=\frac{4(a+b)\pm\sqrt{16(a^2+b^2-ab)}}{24}\\x=\frac{4(a+b)-4\sqrt{a^2+b^2-ab}}{24}$
$x=\frac{a+b-\sqrt{a^2+b^2-ab}}{6}$

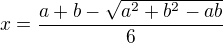
Druhý kořen s + nevyhovuje protože x by bylo větší jak b/2 - což nelze z podstaty věci.
A to je celé