Matematické Fórum

malarad · 16. 02. 2016 10:33

Ahoj, prosím o pomoc s příkladem:
Nevím, jak na to
//forum.matweb.cz/upload3/img/2016-02/15186_z%25C3%25A1po%25C4%258Dtov%25C3%25BD%2Bp%25C5%2599%25C3%25ADklad%2Bz%2Bline%25C3%25A1rn%25C3%25AD%2Balgebry.JPG

Rumburak

↑ malarad:

Ahoj.

Rozložit takovýto ne právě triviální polynom 6-tého stupně na součin kořenových činitelů je bez dalších informací obtížné.
Zadání úlohy však jednu takovou informaci nabízí. Ověřit, zda komplexní číslo $\alpha = 1 + i$ je kořenem daného polynomu
(tj. provést zkoušku dosazením), už tak těžké není. Až budeš mít hotový tento krok, bude mít smysl pouštět se dál.

EDIT. Ale je možno postupovat ještě o něco efektivněji. Předpokládejme, že číslo $\alpha = 1 + i$ skutečně je kořenem
daného polynomu 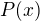$P(x)$ . Jde o polynom s reálnými koeficienty, takže jeho dalším kořenem bude číslo $\beta = 1 - i$
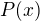(komplexně sdružené s $\alpha$ ). Potom ovšem polynom $P(x)$ bude dělitelný polynomem $Q(x) = (x - \alpha)(x - \beta)$
(což je polynom s reálnými koeficienty). Vydělme polynom 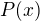$P(x)$ polynomem $Q(x)$ . Vyjde-li dělení beze zbytku, tedy
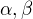polynom $R(x)$ čtvrtého stupně, bude tím zpětně ověřeno, že $\alpha, \beta$ vskutku jsou kořeny polynomu 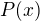$P(x)$ . Zbývajícími
kořeny polynomu 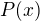$P(x)$ budou kořeny polynomu $R(x)$ .

vanok · 16. 02. 2016 11:56

Ahoj ↑ malarad:,
Okamzite ta mozu napadnut dve metody .
Prva,
Testuj ci1+i je koren
A vyuzi toto: ak 1+ i je koren tak potom aj 1-i je automaticky tiez koren.
Cize potom dany polynom je delitelny z x^2-2x+2...vydel ho a z vysledkom opakuj metodu tolko krat pokial mozne....

Druha metoda
Vyuzi, ze ak $\alpha$ je dvojnasobny koren tak $P(\alpha)=P'(\alpha)=0$
Podobna veta plati pre viacnasobne korene.

vanok · 16. 02. 2016 11:59

↑ Rumburak:,
Pozdravy,
Vidim ze sme spolu pisali. Necham aj moj prispevok. Vsak sa doplnujeme.
Pekny den.

malarad · 16. 02. 2016 12:45

↑ Rumburak: ↑ vanok:
já se na to pak vrhnu, teď bohužel nemám čas.. zatím vám moc děkuju za odpovědi

Rumburak · 17. 02. 2016 09:27

↑ vanok:

Pěkný den i Tobě.

Ano, získá-li autor dotazu širší přehled, tím lépe.

Matematické Fórum

#1 16. 02. 2016 10:33

kořen polynomu

#2 16. 02. 2016 10:58 — Editoval Rumburak (16. 02. 2016 11:26)

Re: kořen polynomu

#3 16. 02. 2016 11:56

Re: kořen polynomu

#4 16. 02. 2016 11:59

Re: kořen polynomu

#5 16. 02. 2016 12:45

Re: kořen polynomu

#6 17. 02. 2016 09:27

Re: kořen polynomu

Zápatí