Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 11. 2015 23:05
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Úloha na "jednoduché rovnice"
Zdravím,
v sekci ZŠ jsme řešili úlohu (zadání opravuji po konzultaci):
Vašek označoval hranice pozemku. Každých 2,5m zapíchne tyč. Najednou unese 8 tyči. Jakou celkovou dráhu minimálně musí ujít, má-li tyče položené v jednom z rohu pozemku a pozemek má tvar čtverce o straně 20m? Vašek chodí pouze po obvodu pozemku a po ukončení práce musí být zpět v rohu pozemku, kde původně ležely tyče.
Je možné jinak, než zkoušením různých variant, prokázat, že nalezené řešení je opravdu minimální (i mimo prostředky ZŠ) + bonus "lze sestavit jednoduchou rovnici pro řešení úlohy"? Děkuji, nehoří.
----------
"Příklad to tak jako tak není. Je to úloha (jestli je nebo není slovní, to je druhá věc)". (c)
Offline
#2 18. 02. 2016 21:22
- mathieux95

- Zelenáč
- Příspěvky: 1
- Pozice: student
- Reputace: 0
Re: Úloha na "jednoduché rovnice"
sú vlastne dve možnosti riešenia. ak budeme nad tým trošku pouvažovať. Ak sa vracia po tyče - tak či sa vracia po UŽ otyčovaných stranách alebo nie. Ak áno (vracia sa po otyčovaných) tak to vychádza viac a to (16 x 20= 320m) ale, ak nie (vracia po neotyčovaných stranách pozemku) vychádza to nasledovne (12 x 20=240m).
Offline
#3 18. 02. 2016 23:41
Re: Úloha na "jednoduché rovnice"
Asi jsem úplně nedodržel zadání, ale když už jsem se s tím sepsal...
Shrnutí:
1) Musí navštívit
 a
a  , to si vynutí
, to si vynutí 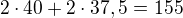 metrů (přitom navštíví a pokryje i šedý->červený vrchol čtverce).
metrů (přitom navštíví a pokryje i šedý->červený vrchol čtverce).2) Musí pokrýt fialový vrchol, to si vynutí
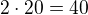 metrů.
metrů.3) Musí pokrýt šedý->modrý vrchol, to si vynutí
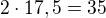 metrů.
metrů.Celkem tedy potřebuje alespoň 230 metrů.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#4 19. 02. 2016 11:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Úloha na "jednoduché rovnice"
Zdravím a děkuji velice za příspěvky, kolegové ↑ mathieux95: a ↑ byk7:.
Kolegovi Ondrovi ještě poděkování za provedení a odměna v podobě asociovaného autora. Ještě jsem nepochopila, jaký je rozdíl, když na závěr (potřebuje 15 tyček) ponese nejdřív 7 nebo 8. Když půjde (pro levou polovinu obrázku) na závěr nejdřív do  , tak ponese co nejvíce - tedy 8. Těch 7 tyček ponese vždy na závěr na úplně posledním úseku (modrém), jelikož 8. tyčku nosit nemusí. Nebo jak?
, tak ponese co nejvíce - tedy 8. Těch 7 tyček ponese vždy na závěr na úplně posledním úseku (modrém), jelikož 8. tyčku nosit nemusí. Nebo jak?
A teď dotaz - lze postup zobecnit na libovolný čtverec o straně  o libovolném počtu dělení
o libovolném počtu dělení  a libovolném počtu tyček
a libovolném počtu tyček  , co může najednou nést. Tj. odvodit vzorec pro standardizaci optimální práce Vaška na libovolném pozemku (čtvercovém, ale tipuji, že na libovolný tvar známého obvodu) ? :-) Ještě děkuji a samozřejmě ani teď nehoří.
, co může najednou nést. Tj. odvodit vzorec pro standardizaci optimální práce Vaška na libovolném pozemku (čtvercovém, ale tipuji, že na libovolný tvar známého obvodu) ? :-) Ještě děkuji a samozřejmě ani teď nehoří.
--------------
"Existují dokonce i zobecnění Fermatova bodu pro čtyřúhelníky. Možná by toto byla reálná alternativa pro řešení zadané úlohy". (c)
Offline

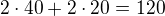 metrů.
metrů.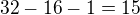 tyčí, tedy musí jít více než jednou a dvakrát to stačí (8+7=15). Jistě ujde více než
tyčí, tedy musí jít více než jednou a dvakrát to stačí (8+7=15). Jistě ujde více než 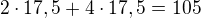 metrů (musí jít dvakrát přes červenou a čtyřikrát přes modrou úsečku.) Teď je otázka, jestli má jít prvně se sedmi a podruhé s osmi, nebo naopak.
metrů (musí jít dvakrát přes červenou a čtyřikrát přes modrou úsečku.) Teď je otázka, jestli má jít prvně se sedmi a podruhé s osmi, nebo naopak. 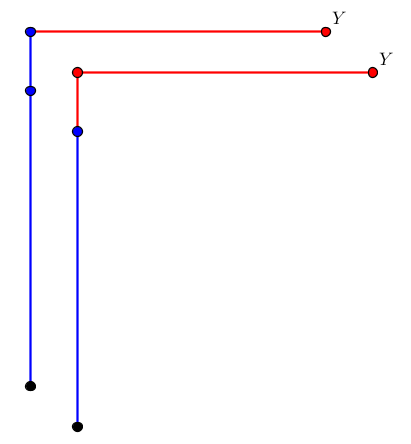
 metrů, přičemž tato hodnota je dosažitelná.
metrů, přičemž tato hodnota je dosažitelná.