Matematické Fórum

FinAAAL · 04. 05. 2009 16:39

Hoj lidičky :-) pomůže mi někdo s řešením těchto příkladů?

1. V geometrické posloupnosti a1=2^-6 , q= 2. Urči n tak, aby platilo $http://www.sitmo.com/gg/latex/latex2png.2.php?z=100&eq=a_n%20%2B%20a_2n%20%3D%208200%20%20$ u toho a2n je 2n v indexu.

2. Součet tří po sobě jdoucích členů geometrické posloupnosti je 9. První člen necháme, druhý zvětšíme o 12 a třetí zmenšíme o 3. Dostaneme tím tři po sobě jdoucí členy aritmetické posloupnosti. Urči původní trojici čísel.

3. Délky hran kvádru tvoří tři po sobě jdoucí členy geometrické posloupnosti, součet délek všec hran kvádru je 84cm. Urči povrch kvádru, je-li objem 64cm3.

4. V geometrické posloupnosti je a1 = 36, urči q tak aby platilo $http://www.sitmo.com/gg/latex/latex2png.2.php?z=100&eq=s_3%20%5Cle%20252$

Díky moc :-)

Ivana · 04. 05. 2009 16:56

↑ FinAAAL:

3.příklad :

Chrpa · 04. 05. 2009 17:07

↑ FinAAAL:
Př2)
Když upravíme tu aritmetickou řadu dostaneme její součet
9 + 12 - 3 = 18
Pak platí:
a_1 + a_1 + d + a_1 + 2d = 18
3a_1 + 3d= 18
a_1 + d = 6
Druhý člen aritmetické posloupnosti = 6
Druhý člen původní geometrické psloupnosti tedy bude: 6 - 12 = -6
Pro geometrickou posloupnost platí:
$a_{n-1}\cdot a_{n+1}=a_n^2$
V našem případě:
$a_1\cdot a_3=a_2^2\nla_1\cdot a_3=36$
Druhá rovnice bude: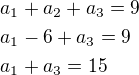
$a_1+a_2+a_3=9\nla_1-6+a_3=9\nla_1+a_3=15$ máme dvě rovnice
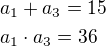$a_1+a_3=15\nla_1\cdot a_3=36$ řešením je:
$a_1=12\nla_1=3$
Dopočítáme poslední člen a_3
pro a_1 = 12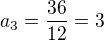
$a_3=\frac{36}{12}=3$
Pro a_1= 3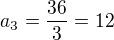
$a_3=\frac{36}{3}=12$

Původní čísla jsou: 3, -6, 12

Ivana · 04. 05. 2009 17:13

↑ FinAAAL:

4.příklad :

Ivana · 04. 05. 2009 17:23

↑ FinAAAL:

řešení ke 4.př.:

Autor skryl část textu. Zobrazit/skrýt!

marnes · 04. 05. 2009 17:47

↑ FinAAAL:
1) budu členy posl značit s velkým A:-)
An+A2n=8200
An+An.q^n=8200
An(1+q^n)=8200
A1.q^(n-1)(1+q^n)=8200 dosadíme za A1 a q
2^-6.2^(n-1)(1+2^n)=8200
2^n(1+2^n)=1 049 600
(2^n)^2+2^n-1 049 600=0 zavedu sub a řeším kvadr rovnici
y^2+2y-1 049 600=0
y1=1024
y2= mínus něco nevyhovuje

2^n=1024
n=10 Kontrola vyjde

FinAAAL · 04. 05. 2009 18:09

ty jo :-D díky moc všichni ;) já se tedy mořim hodiny :-(

FinAAAL · 04. 05. 2009 18:38

↑ marnes:↑ marnes:

An+A2n=8200
An+An.q^n=8200

prosím tě jak si odvodil to A2n na An. q^n ?

marnes · 04. 05. 2009 20:11

↑ FinAAAL:

As=Ar.q^(s-r) s=2r
A2r=Ar.q^(2r-r)
A2r=Ar.q^r

((:-)) · 27. 01. 2013 15:14 — Editoval ((:-)) (27. 01. 2013 15:16)

↑ Maths:

Ahoj. Dávaš otázku v dávno vyriešenej téme z roku 2009 človeku, ktorý sem v tejto podobe už vôbec nechodí ...

A myslím si, že by si sa mala pýtať na konkrétny krok, ktorému nerozumieš, nie že nerozumieš ničomu...

Elisa · 14. 02. 2016 21:47

Dobrý den, proč je prosím u příkladu 2) součet 18 - nechápu, jak se získá součet aritm. posloupnosti jakou součet stejných členů goniometrické + jejich zvětšení. A proč je 2. člen geomet. poslupnosti -6, když je aritm. člen 6? Moc děkuji

vanok · 14. 02. 2016 22:35 — Editoval vanok (14. 02. 2016 23:25)

Ahoj ↑ Elisa:,
Vsak vies ze sucet troch clenov geomertickej postupnosti je 9.
Ked pridat 12 a potom -3 dostanes sucet clenov aritmetickej postupnosti, cize18

Potom g2= a 2 - 1 2
( g... Geom. a.....Aritm)
Tiez vies ze ked mas tri susedne cleny arit.postupnosti su take ze a1+a3=2a2 ( stredny je arithmeticky priemer dvoch koncovych)

Elisa · 14. 02. 2016 22:42

↑ vanok:
Děkuji, ale já nevím, jaká je souvislost mezi členy aritmetické a geometrické posloupnosti.
Počítala jsem to jako soustavu 3 rovnic o 3 neznámých a1, a2, a3
v jedné byl součet geometrické posloupnosti = 9
další dvě byly definice aritmetické a geometrické posloupnosti - stejný rozdíl a stejný podíl
Jde to takto (nevyšlo mi to)?

vanok · 14. 02. 2016 22:45

↑ Elisa:,
Ide ale to co pisem je rychlejsie

vanok · 14. 02. 2016 22:56

Inac v tom texte je riesenie trochu nelogicke z tym ich oznacenim. Tam a1,a2,a3 su geom postupnost. Tak to je potrebne dobre dat do poriadku

Cheop · 16. 02. 2016 07:54 — Editoval Cheop (16. 02. 2016 12:46)

↑ Elisa:
Jde to i tak jak píšeš v příspěvku 13 tedy: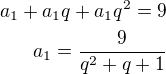
$a_1+a_1q+a_1q^2=9\\a_1=\frac{9}{q^2+q+1}$ součet prvních tří členů GP = 9
$a_2=\frac{9q}{q^2+q+1}\\a_3=\frac{9q^2}{q^2+q+1}$ další 2 členy GP
Teď vyjádříme členy AR dle zadání tj.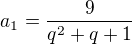
$a_1=\frac{9}{q^2+q+1}$ první člen AR necháme
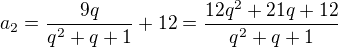$a_2=\frac{9q}{q^2+q+1}+12=\frac{12q^2+21q+12}{q^2+q+1}$ - druhý člen zvětšíme o 12
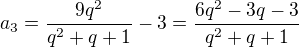$a_3=\frac{9q^2}{q^2+q+1}-3=\frac{6q^2-3q-3}{q^2+q+1}$ - třetí člen zmenšíme o 3
Rozdíl mezi druhým a prvním členem AP resp. mezi třetím a druhým členem musí být stejný diference d tedy: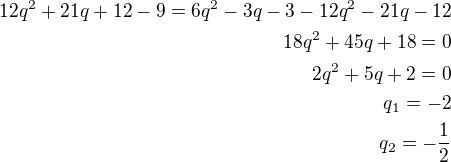
$12q^2+21q+12-9=6q^2-3q-3-12q^2-21q-12\\18q^2+45q+18=0\\2q^2+5q+2=0\\q_1=-2\\q_2=-\frac 12$
A nyní stačí dopočítat původní člen a_1 GP resp. a_2 a a_3
Pro 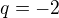$q=-2$
$a_1=\frac{9}{q^2+q+1}=\frac{9}{4-2+1}=3\\a_2=a_1\cdot q=3\cdot(-2)=-6\\a_3=a_2\cdot q=-6\cdot(-2)=12$
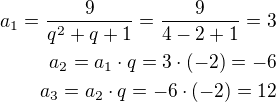
Původní čísla jsou:
3, -6, 12
PS pokud použijeme $q=-\frac 12$ pak dostaneme stejné členy jen v obráceném pořadí