Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 02. 2016 20:46
Limitny maraton
Pozdravujem,
Casto vidime na tomto fore tazkosti s riesenim cviceni tykajucich sa klasickych limit.
Tak tu navrhujem riesit limity, ktore ste mohli stretnut pri roznych skuskach.
Pozor cakam tu na dokonale riesenia takych cviceni. Tak aby citatel po ich citani uz nemal ziadne otazky.
Pripominam, ze na vela forach, princip maratonu je, ze posledny riesitel navrhne nove cvicenie.
Tak cvicenie 1
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 17. 02. 2016 15:23
Re: Limitny maraton
Riesenie cvicenia 1.
Pre dostatocne male ostro kladne x mame 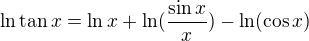 .
.
Pretoze ( dobre vieme, ze ) 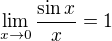 ako aj
ako aj 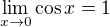
Mame  a tiez
a tiez 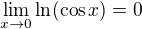
Co da pochopitelne  a tiez
a tiez  .
.
Na koniec pre  je
je  , a ( dobre vieme, ze)
, a ( dobre vieme, ze) 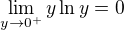 a tu
a tu 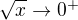 ked
ked  , co nam da
, co nam da  .
.
Predosle vysledky nam daju 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 18. 02. 2016 13:24 — Editoval vanok (18. 02. 2016 13:26)
Re: Limitny maraton
Akoze som riesil predosle cvicenie, tak pridavam
Cvicenie 2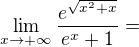
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 18. 02. 2016 15:40
Re: Limitny maraton
↑ vytautas:
Zdravím.
Nezdá se mi, že by mělo platit ,
,
jak je použito v prvním řádku.
Pokud se tedy nemýlím.
Offline
#6 18. 02. 2016 15:50 — Editoval vanok (18. 02. 2016 15:53)
Re: Limitny maraton
↑ vytautas:
Ahoj, skus opravit tvoje riesene.
V prvej rovnosti , ( prvy riadok, citalel ) mas chybu .
Edit. Vidim ze kolega, Jj ( pozdravujem) napisal tu chybu explicitne.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 20. 02. 2016 00:23
Re: Limitny maraton
↑ vanok:
Už snáď správne riešenie.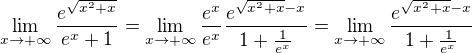
Podľa rastovej škály 
Takže podľa aritmetiky limít 
Ďalej 
Keďže 
Podľa vety o limite zloženej funkcie s podmienkou S ( je spojitá na svojom def. obore, čiže aj v
je spojitá na svojom def. obore, čiže aj v  )
)
Potom 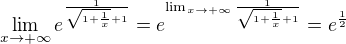
Cvicenie 3 
Per aspera ad astra
Offline
#8 20. 02. 2016 12:12 — Editoval Brzls (20. 02. 2016 21:46)
Re: Limitny maraton
Offline
#9 20. 02. 2016 15:12 — Editoval Bati (22. 02. 2016 08:46)
Re: Limitny maraton
Řešení cvičení 4:
Cvičení 5:
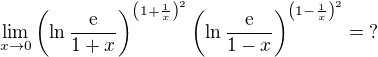
Nápověda:
Offline
#10 21. 02. 2016 23:33 — Editoval Freedy (21. 02. 2016 23:52) Příspěvek uživatele Freedy byl skryt uživatelem Freedy. Důvod: -.- fail
#12 22. 02. 2016 09:05 Příspěvek uživatele Bati byl skryt uživatelem Bati. Důvod: Už zbytečné
#13 22. 02. 2016 10:17 — Editoval Freedy (22. 02. 2016 11:38)
Re: Limitny maraton
↑ Bati:
Mate pravdu, pardon, svuj postup opravim, vecer mi to asi nejak nemyslelo ;-)
Bati napsal(a):
protože
neexistuje.
pro korekci, tuto limitu jsem tam nevyšetřoval. Ve jmenovateli bylo pouze x, nikoliv x^2.
Nicméně byla chyba již v úvodu ;) a celkem trapná, nicméně nápad již nějaký mám, ale momentálně nemám čas, večer to zkusím opravit.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#14 23. 02. 2016 18:13
Re: Limitny maraton
Pozdravujem,
Vlakno sa rozbehlo.
Navrhujem este, aby ostalo dynamicke, bolo by dobre, ze ak nejake cvicenie je bez dobreho riesenia, pocas 5, 6 dni, aby jeho autor dal jeho vlastne riesenie.( a ho dat aj vtedy, ak myslel na ine riesenie ako to, ktore je urobene na fore).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 26. 02. 2016 11:30 — Editoval Bati (26. 02. 2016 11:31)
Re: Limitny maraton
Protože cvičení 5 dosud nikdo nevyřešil, napíšu sem svoje řešení a počkám jestli někdo zareaguje. Nechtěl jsem to tu takhle zazdít, jen jsem chtěl vymyslet nějakou limitu, na kterou neplatí klasický finty :-)
Řešení cvičení 5:
Offline
#16 26. 02. 2016 12:34
Re: Limitny maraton
Ahoj ↑ Freedy:,
Iste vies, ze na chybach sa da vela naucit. To je skoda, ze si skryl tvoj pokus riesenia. Kolegom mohlo byt uzitocne analyzovat tvoju chybu a potom nerobit podobne chyby pri skuskach.
Dobre pokracovanie a vela pokrokov.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 26. 02. 2016 21:45
Re: Limitny maraton
↑ Bati:
Řešení cvičení 5 s použitím klasických fint a bez použití derivací: :-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#19 27. 02. 2016 18:24
Re: Limitny maraton
Pozdravujem, Bati, Pavel jeden z vas by mal dat cvicenie 6 ( pripadne aj cvicenie 7) aby pokracovala dynamika vlakna.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#21 01. 03. 2016 18:13 — Editoval Freedy (01. 03. 2016 18:22)
Re: Limitny maraton
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#22 08. 03. 2016 10:45 — Editoval vanok (08. 03. 2016 11:40)
Re: Limitny maraton
Ahoj ↑ Freedy:,
Akoze nikoho nezaujalo tvoje cvicenie, bolo by dobre aby si dal tvoje riesenie a tiez aj nove cvicenie take ake mohlo byt dane na nejakej skuske.
Tiez je skoda ze dvaja riesitelia po rieseni nedali ziadne cvicenie.
Dufam, ze sa toto vlakno ozivi a dynamizuje.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#23 09. 03. 2016 12:07 — Editoval Marian (09. 03. 2016 12:08)
Re: Limitny maraton
↑ Freedy:
Nerad bych kazil radost z výpočtu úlohy, ale tato limita se již probírala na fóru a dokonce i v sekci zajímavých úloh z matematické analýzy, viz tento odkaz.
Je ovšem docela možné, že někdo přijde s jiným přístupem a rovněž vyřeší danou limitu.
Offline
#24 09. 03. 2016 12:31
Re: Limitny maraton
↑ Marian:,
Pozdravujem,
Dakujem, ze ta zaujalo toto vlakno, mozes tu dat jednu z tvojej zasoby limit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#25 09. 03. 2016 13:57
Re: Limitny maraton
Pozdravujem,
Pridavam jedno cvicenie.
No len preto aby tu ostala dynamika a aby citatelia studenty mohli sa poucit.
Ti co zatial nedali cvicenia, po rieseni predoslych cviceni, nech nevahaju.
O cviceni, co nasleduje, mozno mi poviete, ze je to trochu sadizmus, no ale na koniec je skor jednoduche.
cvicenie 8
Vysetrite limitu, ak existuje 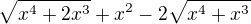 pre
pre 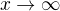
( najdene na webe)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

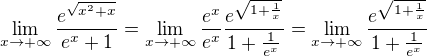
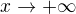
 je spojitá v
je spojitá v  , tak riešim len argument, čiže
, tak riešim len argument, čiže 
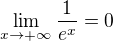

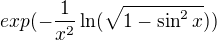



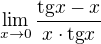
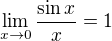 , spojitosti funkce kosinus v 0 a věty o aritmetice limit dostaneme
, spojitosti funkce kosinus v 0 a věty o aritmetice limit dostaneme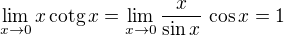 .
.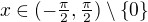 platí
platí .
. ,
, .
.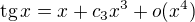 pro
pro  . Odtud již vidíme, že
. Odtud již vidíme, že  .
. dvěma způsoby, kde
dvěma způsoby, kde 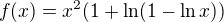 .
.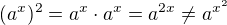
 a pro
a pro  počítejme první a druhou derivaci:
počítejme první a druhou derivaci: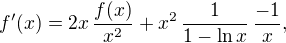
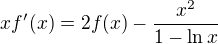 .
. .
.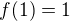 a z (1) a (2) snadno dostáváme
a z (1) a (2) snadno dostáváme 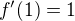 ,
,  . Protože
. Protože 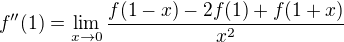 , neboť podle Taylorovy věty máme
, neboť podle Taylorovy věty máme
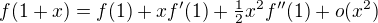 , a tedy
, a tedy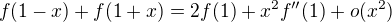 .
.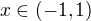 platí
platí ,
,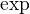 dostáváme konečně
dostáváme konečně .
.
 vyšetřovanou limitu, tj.
vyšetřovanou limitu, tj.
![kopírovat do textarea $
\ln L&=\lim_{x\to0}\left[\(1+\frac1x\)^2\ln\bigl(1-\ln(1+x)\bigr)+\(1-\frac1x\)^2\ln\bigl(1-\ln(1-x)\bigr)\right]\\[.5\baselineskip]
&=\lim_{x\to0}\left[\(1+\frac 2x+\frac1{x^2}\)\ln\bigl(1-\ln(1+x)\bigr)+\(1-\frac 2x+\frac1{x^2}\)\ln\bigl(1-\ln(1-x)\bigr)\right]\\[.5\baselineskip]
&=\underbrace{\lim_{x\to0}\left[\ln\bigl(1-\ln(1+x)\bigr)+\ln\bigl(1-\ln(1-x)\bigr)\right]}_{L_1}+\\[.5\baselineskip]
&\quad\underbrace{\lim_{x\to0}\frac 2x\left[\ln\bigl(1-\ln(1+x)\bigr)-\ln\bigl(1-\ln(1-x)\bigr)\right]}_{L_2}+\\[.5\baselineskip]
&\quad\underbrace{\lim_{x\to0}\frac 1{x^2}\left[\ln\bigl(1-\ln(1+x)\bigr)+\ln\bigl(1-\ln(1-x)\bigr)\right]}_{L_3}\\[.5\baselineskip]
$](/mathtex/e8/e88cec44b07f6fa6b54a59f4df720a77.gif)
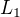 ,
, 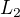 a
a 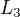 :
:![kopírovat do textarea $
{\color{blue}L_1}&=\lim_{x\to0}\left[\ln\bigl(1-\ln(1+x)\bigr)+\ln\bigl(1-\ln(1-x)\bigr)\right]=0+0={\color{blue}0}\\[\baselineskip]
{\color{blue}L_2}&=\lim_{x\to0}\frac 2x\left[\ln\bigl(1-\ln(1+x)\bigr)-\ln\bigl(1-\ln(1-x)\bigr)\right]
=2\lim_{x\to0}\frac{\ln\bigl(1-\ln(1+x)\bigr)}x-2\lim_{x\to0}\frac{\ln\bigl(1-\ln(1-x)\bigr)}x\\[.5\baselineskip]
&=2\lim_{x\to0}\frac{\ln\bigl(1-\ln(1+x)\bigr)}{\ln(1+x)}\cdot\lim_{x\to0}\frac{\ln(1+x)}x-2\lim_{x\to0}\frac{\ln\bigl(1-\ln(1-x)\bigr)}{\ln(1-x)}\cdot\lim_{x\to0}\frac{\ln(1-x)}x\\[.5\baselineskip]
&=2\cdot(-1)\cdot 1-2\cdot(-1)\cdot(-1)={\color{blue}-4}\\[\baselineskip]
{\color{blue}L_3}&=\lim_{x\to0}\frac 1{x^2}\left[\ln\bigl(1-\ln(1+x)\bigr)+\ln\bigl(1-\ln(1-x)\bigr)\right]
=\lim_{x\to0}\frac{\ln\left[\bigl(1-\ln(1+x)\bigr)\cdot\bigl(1-\ln(1-x)\bigr)\right]}{x^2}\\[.5\baselineskip]
&=\lim_{x\to0}\frac{\ln\left[\bigl(1-\ln(1+x)\bigr)\cdot\bigl(1-\ln(1-x)\bigr)\right]}{1-\bigl(1-\ln(1+x)\bigr)\cdot\bigl(1-\ln(1-x)\bigr)}\cdot\lim_{x\to0}\frac{1-\bigl(1-\ln(1+x)\bigr)\cdot\bigl(1-\ln(1-x)\bigr)}{x^2}\\[.5\baselineskip]
&=-1\cdot\lim_{x\to0}\frac{1-\bigl(1-\ln(1+x)\bigr)\cdot\bigl(1-\ln(1-x)\bigr)}{x^2}\\[.5\baselineskip]
&=-\lim_{x\to0}\frac{\ln(1+x)+\ln(1-x)}{x^2}+\lim_{x\to0}\frac{\ln(1+x)\cdot\ln(1-x)}{x^2}\\[.5\baselineskip]
&=-\lim_{x\to0}\frac{\ln(1-x^2)}{x^2}+\lim_{x\to0}\frac{\ln(1+x)}{x}\cdot\lim_{x\to0}\frac{\ln(1-x)}{x}=-(-1)+1\cdot(-1)={\color{blue}0}
$](/mathtex/d7/d74967909c09ffeb57e012d865b139c3.gif)


![kopírovat do textarea $\lim_{x\rightarrow \infty}\left[\frac{\ln(x^2+3x+4)}{\ln(x^2+2x+3)}\right]^{x\ln x}$](/mathtex/d7/d745a5ad783ccb6e474dbcc2789d0cd0.gif)
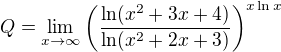
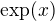 je spojitá na celém definičním oboru a platí:
je spojitá na celém definičním oboru a platí: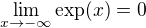
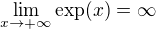

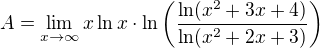
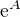
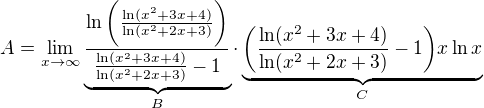

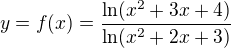
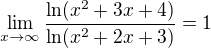
 splňuje podmínku P, jelikož
splňuje podmínku P, jelikož 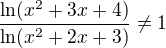 na
na 
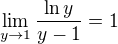 podle známé limity.
podle známé limity.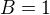
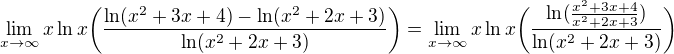

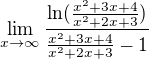

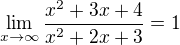 a je splněna podmínka P
a je splněna podmínka P 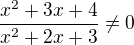 na
na 

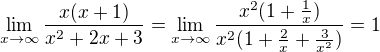
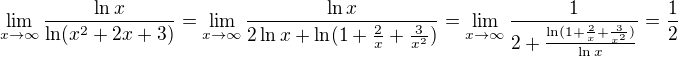


 ,
,