Matematické Fórum

Everald · 27. 05. 2008 19:12

Zdravím,

potřebuji vyšetřit průběh této fce:

arcsin(((1+x)/(1-x)))

a zaksl jsem hnedle u def. oboru:

arcsin má df <-1,1> pokud doufám správně a pak
-1<=(1+x)/(1-x) a (1+x)/(1-x)<=1

z toho prvni tabulka má pak (-nek, 1) 1 (1, nek)
+ - -
a druhá (-nek,0) 0 (0,1) 1 (1,nek)
- 0 + nd -

v tom případě by mi průnik vyšel jako int. (0,1)

je to správně nebo mám někde sek?

robert.marik · 27. 05. 2008 19:36

http://wood.mendelu.cz/math/maw/gnuplot … ko=Odeslat

v tom zapise se nevyznam, ale ten link vede na graf funkce (1+x)/(1-x), odkud jde videt, ze resenim soutavy nerovnic

-1<=(1+x)/(1-x)<=1 je interval (-nekonecno, 0]

Everald · 27. 05. 2008 20:04

chjo, už jsem přišel na to co jsem udělal špatně...
špatně jsem odečítal z tabulek, neuvažoval jsem že když je výraz větší jak 0 tak beru kladné hodnoty a když je menší jak 0 tak beru ty záporné :-)

takže nakonec je to tedy jak píšeš a to (-nek, 0)

a další věcí je jak učit nulový bod... sice vím že je to -1 ale jak jej dokázat?

plisna · 27. 05. 2008 20:29

protoze $\arcsin \left( \frac{1+x}{1-x} \right) = 0 \qquad \Leftrightarrow \qquad \frac{1+x}{1-x} = 0 \qquad \Rightarrow \qquad x = -1$

Everald · 27. 05. 2008 20:44

Další otázka:
potřebuji zjistit intervaly monotónie a lokální extrémy, to znamená, že nejprve určit nulový bod(y) a to zjistím z první derivace.

První derivaci jsem zmákl:

1/((x-1)*odm(-x)) -- po úpravách

pak to položím rovno 0

mno a tím jsem zase skončil, buď žádné body nejsou což nevím jak určit intervaly? Případně nějak upravit ten výraz?

plisna · 27. 05. 2008 20:48

a co je pro tebe nulovy bod? bod, ve kterem je funkcni hodnota nulova (bod, kde funkce protina osu x) a nebo bod, ve kterem je prvni derivace nulova (stacionarni bod)?

Everald · 27. 05. 2008 20:50

tak je to stacionární bod, promiň.

Everald · 27. 05. 2008 20:56

mno pokročil jsem dále a udělal druhou derivaci, z ní potřebuji zjistit konvexnost, konkalnosta inflexní bod(y).

derivaci sem psát nebudu to bych zblbl, ale když ji položím rovno nule, co pak s tím? co z toho výrazu vlastně položit rovno nule a na čem to závisí?

zde je odkaz na výpočet

plisna · 27. 05. 2008 21:01

ale ta funkce zadne stacionarni body nema!

Everald · 27. 05. 2008 21:07

Mno asi zi zopaknu co to ty body jsou, ale zatím díky.

A ta konvexnost a konkálnost?

plisna · 27. 05. 2008 21:09

konvexnost a konkavnost se urci podle znamenek druhe derivace. ale nebude moc prijemne to derivovat a nasledne dopocitavat.

Everald · 27. 05. 2008 21:12

No i druhou derivaci mám, a odkaz na výsledek je výše, alenevím jak určit pokaždé ty body, sice jsem nějaký spočítal a vyšel 1/3, ale nevím jestli to je správně když je to mimo interval def. oboru.

Everald · 27. 05. 2008 22:11

kdyby se mi někdo mrknul naty konvexnost a konkálnost a ta body co patři do téhle sekce, byl bych vděčen...

robert.marik

↑ Everald:
jestli je ta druha derivace dobre, tak ta funkce kriticke body nema (x=1/3, coz by pripadalo v uvahu jako nulovy bod druhe derivace, se pochopitelne nepocita).

Protoze funkce na definicnim oboru nema ani body nespojitosti, je bud porad konvexni nebo porad konkavni.

Ktera z techto moznosti plati se pozna z vypoctu druhe derivace v libovolnem bode z definicniho oboru, treba y''(-1)

Everald · 27. 05. 2008 22:26

takže když je výsledek záporný, tak je fce konkální, že? inflexní body nemá, ale kritické? to ani netuším že jsou...

robert.marik

Kritický bod je bod kde je nulová derivace, je tam podezření že bz tam mohl být inflenxní bod. Možná máte jinou terminologii.

Takže vychází že fukce je klesající a konkávní..... Podle obrázku to tak ale nevypadá, že? !!!!!!!!!

Arkussinus se po derivaci spatne upravuje, pokud tam nejak zjednodusujeme ty odmocniny. V dusledku toho jsou ty derivace vypoctene tim vasim odkazem bohuzel spatne ....

O.K. Maxima selhava, zkusil jsem na calc101.com co s tim udela Mathematica a ta cpe do drueh deriavce imaginarni jednotku, takze zase nic .... asi nezbude nez derivace spocitat znovu a opatrne a rucne .... bohuzel.

spravna derivace je 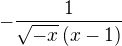$-\frac{1}{\sqrt{-x}\,(x-1)}$

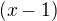pri uprave pocitac totiz upravi $\sqrt{(x-1)^2}$ na $(x-1)$ , což ostatně dělají často i studenti a je to chyba.

druha derivace: $\frac{\sqrt{-x}\,\left( 3\,x-1\right) \,|x-1|}{2\,{\left( x-1\right) }^{3}\,{x}^{2}}$

Tak ted uz to snad pujde, diky za objeveni te chyby, zjistim jestli to je chyba te moji aplikace nebo chyba Maximy a nejak to zkusim poresit. aspon mame pouceni, ze pocitacum se opravdu zas tak moc verit nema .....

Everald · 27. 05. 2008 23:10

taky jsem si říkal, že podle toho obrázku to nevychází, zkusím si to bez té posledn úpravy výrazu... prozatím díky

Everald · 28. 05. 2008 09:10

ještě by mě zajímalo proč je o toho vyrazu vlastně to mínus?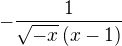

$-\frac{1}{\sqrt{-x}\,(x-1)}$

já to sice spočítal ale vyšlo to plusově... pokud chápu robera.marika:

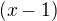"" $\sqrt{(x-1)^2}$ na $(x-1)$ , což ostatně dělají často i studenti a je to chyba ""

tak výsledek by měl být : $-(x-1)$ , bohužel jsem se s tím nesetkal, resp. pokud ano tak jsem tam určitě to mínus nedal.

robert.marik

$\sqrt{(x-1)^2}=|x-1|$

protoze je x zaporne (viz definicni obor), je x-1 take zaporne a plati: |x-1|=-(x-1)=1-x

Napalm · 19. 04. 2009 23:05

A jaký byl pak ten inflefní bod?

Matematické Fórum

#1 27. 05. 2008 19:12

Vyšetřit průběh fce s arcsin

#2 27. 05. 2008 19:36

Re: Vyšetřit průběh fce s arcsin

#3 27. 05. 2008 20:04

Re: Vyšetřit průběh fce s arcsin

#4 27. 05. 2008 20:29

Re: Vyšetřit průběh fce s arcsin

#5 27. 05. 2008 20:44

Re: Vyšetřit průběh fce s arcsin

#6 27. 05. 2008 20:48

Re: Vyšetřit průběh fce s arcsin

#7 27. 05. 2008 20:50

Re: Vyšetřit průběh fce s arcsin

#8 27. 05. 2008 20:56

Re: Vyšetřit průběh fce s arcsin

#9 27. 05. 2008 21:01

Re: Vyšetřit průběh fce s arcsin

#10 27. 05. 2008 21:07

Re: Vyšetřit průběh fce s arcsin

#11 27. 05. 2008 21:09

Re: Vyšetřit průběh fce s arcsin

#12 27. 05. 2008 21:12

Re: Vyšetřit průběh fce s arcsin

#13 27. 05. 2008 22:11

Re: Vyšetřit průběh fce s arcsin

#14 27. 05. 2008 22:20 — Editoval robert.marik (27. 05. 2008 22:22)

Re: Vyšetřit průběh fce s arcsin

#15 27. 05. 2008 22:26

Re: Vyšetřit průběh fce s arcsin

#16 27. 05. 2008 22:58 — Editoval robert.marik (27. 05. 2008 23:09)

Re: Vyšetřit průběh fce s arcsin

#17 27. 05. 2008 23:10

Re: Vyšetřit průběh fce s arcsin

#18 28. 05. 2008 09:10

Re: Vyšetřit průběh fce s arcsin

#19 28. 05. 2008 09:49 — Editoval robert.marik (28. 05. 2008 09:50)

Re: Vyšetřit průběh fce s arcsin

#20 19. 04. 2009 23:05

Re: Vyšetřit průběh fce s arcsin

Zápatí