Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 01. 03. 2016 11:34 — Editoval Marian (03. 03. 2016 11:41)
Re: Definite integral
The partial answer to the 1st integral...
The answer to the 2nd integral...
Offline
#3 04. 03. 2016 07:52 — Editoval stuart clark (04. 03. 2016 07:54)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Definite integral
Thanks ↑ Marian: for nice explanation.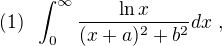 Where
Where 
Offline
#4 04. 03. 2016 08:24 — Editoval Pavel (04. 03. 2016 22:19)
Re: Definite integral
↑ stuart clark:
The last two steps are wrong. It should be
I also tried to solve this integral using multiple integrals and partial derivatives. Unfortunetally, I obtained only the piece of the solution. However I found the interesting integral identity. I will show it later.
Correction: I have completed my calculation and found the integral, see below.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#5 05. 03. 2016 01:43 — Editoval Pavel (05. 03. 2016 18:36)
Re: Definite integral
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
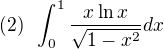


![kopírovat do textarea $
I(0,1)
&=\int_{0}^{1}\frac{\ln (x)}{x^2+1}\mathrm dx
+\int_{1}^{\infty}\frac{\ln (x)}{x^2+1}\mathrm dx\\[2mm]
&=\int_{0}^{1}\frac{\ln (x)}{x^2+1}\mathrm dx
+\int_{1}^{0}\frac{\ln (1/t)}{(1/t)^2+1}\cdot\frac{-1}{t^2}\mathrm dt\\[2mm]
&=\int_{0}^{1}\frac{\ln (x)}{x^2+1}\mathrm dx
-\int_{0}^{1}\frac{\ln (t)}{1+t^2}\mathrm dt
=0.
$](/mathtex/cc/cc134d1aacad717dbcffe000102bd16b.gif)
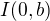 with
with  . We deduce that
. We deduce that![kopírovat do textarea $
I(0,b)
&=\frac{1}{b^2}\int_{0}^{\infty}\frac{\ln (x)}{(x/b)^2+1}\mathrm dx\\[2mm]
&=\frac{1}{b^2}\int_{0}^{\infty}\frac{\ln (bt)}{t^2+1}\cdot b\mathrm dt\\[2mm]
&=\frac{1}{b}\int_{0}^{\infty}\frac{\ln (b)}{t^2+1}\mathrm dt
+\underbrace{\frac{1}{b}\int_{0}^{\infty}\frac{\ln (t)}{t^2+1}\mathrm dt}_{=I(0,1)}.
$](/mathtex/6f/6f889447a84b793beb5eb30b713250b9.gif)
![kopírovat do textarea $
\usepackage[dvipsnames]{xcolor}
{\color{purple}\boldsymbol{I(0,b)=\frac{\pi}{2b}\cdot\ln (b)}}.
$](/mathtex/1b/1b9c18e7c657d904cda9cf25c034f050.gif)
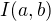 . However, I guess that for
. However, I guess that for 

![kopírovat do textarea $
\int\frac{x\cdot\ln (x)}{\sqrt{1-x^2}}\mathrm dx
&=-\ln (x)\cdot\sqrt{1-x^2}+\sqrt{1-x^2}-\ln (\sqrt{1-x^2}+1)+\ln (x)\\
&=\cdots\\[1mm]
&=\frac{x^2\cdot\ln (x)}{1+\sqrt{1-x^2}}+\sqrt{1-x^2}-\ln\left (\sqrt{1-x^2}+1\right )+C.
$](/mathtex/26/2661b63ac3714e196e4e445db2f6ed46.gif)
![kopírovat do textarea $
\usepackage[dvipsnames]{xcolor}
\int_{0}^{1}\frac{x\cdot\ln (x)}{\sqrt{1-x^2}}\mathrm dx
={\color{purple}\boldsymbol{\ln (2)-1}}.
$](/mathtex/7e/7efcc4b1212391a2f2c43ab7d3beec94.gif)
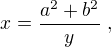 Then
Then 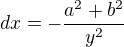 and changing Limits,We get
and changing Limits,We get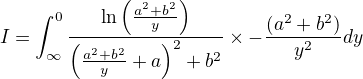
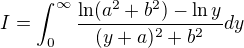
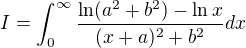
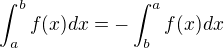 and
and 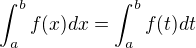
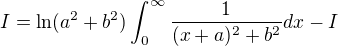
![kopírovat do textarea $2I = \ln(a^2+b^2)\cdot \frac{1}{b}\cdot \left[\tan^{-1}\left(\frac{x+a}{b}\right)\right]_{0}^{\infty}=\frac{\pi}{2b}\cdot \ln(a^2+b^2)$](/mathtex/3a/3a200a11fd99663af1a50c871e134ce8.gif)
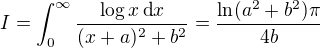
![kopírovat do textarea $
2I = \ln(a^2+b^2)\cdot \frac{1}{b}\cdot \left[\tan^{-1}\left(\frac{x+a}{b}\right)\right]_{0}^{\infty}
={\color{red}\left(\frac{\pi}{2}-\tan^{-1}\left(\frac ab\right)\right)\cdot \frac 12\ln(a^2+b^2)
=\frac 1b\cdot\tan^{-1}\left(\frac ba\right)\cdot\ln(a^2+b^2)}
$](/mathtex/b2/b22d3b23f5b8c1ab0e89eb97a459de5c.gif)

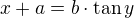 . Then
. Then![kopírovat do textarea $
\int_{0}^{\infty}\frac{\ln x}{(x+a)^2+b^2}\,\mathrm dx
&=\frac 1b\int_{\arctan\frac ab}^{\frac{\pi}2}\frac{\ln(b\cdot\tan y-a)}{\tan^2y+1}\cdot\frac{\mathrm dy}{\cos^2 y}
=\frac 1b\int_{\arctan\frac ab}^{\frac{\pi}2}\ln(b\cdot\tan y-a)\,\mathrm dy\\[.5\baselineskip]
&=\frac 1b\int_{\arctan\frac ab}^{\frac{\pi}2}\ln\left(b\cdot\tan y\left(1-\frac ab\cot y\right)\right)\mathrm dy\\[.5\baselineskip]
&=\frac 1b\biggl(\underbrace{\int_{\arctan\frac ab}^{\frac{\pi}2}\ln b\,\mathrm dy}_{\mathsf I_1}+\underbrace{\int_{\arctan\frac ab}^{\frac{\pi}2}\ln(\tan y)\,\mathrm dy}_{\mathsf I_2}+\underbrace{\int_{\arctan\frac ab}^{\frac{\pi}2}\ln\left(1-\frac ab\cot y\right)\mathrm dy}_{\mathsf I_3}\biggr)
$](/mathtex/0d/0d139e3fe3143cd8f00b5387e8c4973d.gif)
 and
and 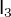 :
:
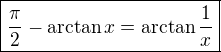 for
for  .
.![kopírovat do textarea $
\mathsf I_3&=\int_{\arctan\frac ab}^{\frac{\pi}2}\ln\left(1-\frac ab\cot y\right)\mathrm dy
=\int_{\arctan\frac ab}^{\frac{\pi}2}\left[\ln\left(1-u\cdot\cot y\right)\right]_{u=0}^{u=\frac ab}\mathrm dy
=\int_{\arctan\frac ab}^{\frac{\pi}2}\int_{0}^{\frac ab}\frac{\partial}{\partial u}\ln(1-u\cdot\cot y)\,\mathrm du\mathrm dy\\[.5\baselineskip]
&=\int_{0}^{\frac ab}\int_{\arctan\frac ab}^{\frac{\pi}2}\frac{\partial}{\partial u}\ln(1-u\cdot\cot y)\,\mathrm dy\mathrm du
=\int_{0}^{\frac ab}\int_{\arctan\frac ab}^{\frac{\pi}2}\frac{-\cot y}{1-u\cdot\cot y}\,\mathrm dy\mathrm du
=-\int_{0}^{\frac ab}\int_{\arctan\frac ab}^{\frac{\pi}2}\frac{1}{\tan y-u}\,\mathrm dy\mathrm du
$](/mathtex/bf/bf3d4527b671cdea8410c0c524efb90c.gif)

![kopírovat do textarea $
\mathsf I_3&=\dots
=-\int_{0}^{\frac ab}\int_{\arctan\frac ab}^{\frac{\pi}2}\frac{1}{\tan y-u}\,\mathrm dy\mathrm du
=-\int_{0}^{\frac ab}\left[\frac 1{1+u^2}\left(\ln|u\cos y-\sin y|-uy\right)\right]_{y=\arctan\frac ab}^{y=\frac{\pi}2}\,\mathrm du\\[.5\baselineskip]
&=\int_{0}^{\frac ab}\frac 1{1+u^2}\left(\frac{\pi}2\,u+\ln\left|u\cos\left(\arctan\frac ab\right)-\sin\left(\arctan\frac ab\right)\right|-u\cdot\arctan\frac ab\right)\,\mathrm du\\[.5\baselineskip]
&=\underbrace{\int_{0}^{\frac ab}\frac 1{1+u^2}\left(\frac{\pi}2\,u-u\cdot\arctan\frac ab\right)\,\mathrm du}_{\mathsf J_1}+\underbrace{\int_{0}^{\frac ab}\frac 1{1+u^2}\ln\left|u\cos\left(\arctan\frac ab\right)-\sin\left(\arctan\frac ab\right)\right|\,\mathrm du}_{\mathsf J_2}
$](/mathtex/bd/bdee3307e428326433650034db10a111.gif)
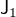 using the first boxed identity:
using the first boxed identity:![kopírovat do textarea $
\mathsf J_1&=\int_{0}^{\frac ab}\frac 1{1+u^2}\left(\frac{\pi}2\,u-u\cdot\arctan\frac ab\right)\,\mathrm du
=\left(\frac{\pi}2-\arctan\frac ab\right)\int_{0}^{\frac ab}\frac {u}{1+u^2}\,\mathrm du
=\arctan\frac ba\cdot\frac 12\int_{0}^{\frac ab}\frac {2u}{1+u^2}\,\mathrm du\\[.5\baselineskip]
&=\arctan\frac ba\cdot\frac 12\left[\ln|1+u^2|\right]_{u=0}^{u=\frac ab}
=\arctan\frac ba\cdot\frac 12\left(\ln\left(a^2+b^2\right)-\ln\left(b^2\right)\right)\\[.5\baselineskip]
&=\arctan\frac ba\cdot\ln\sqrt{a^2+b^2}-\arctan\frac ba\cdot\ln b
=\boldsymbol{\arctan\frac ba\cdot\ln\sqrt{a^2+b^2}-\mathsf I_1}
$](/mathtex/f7/f7168360c220156bb84efe55f0df645a.gif)

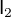 ,
, 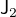 :
:
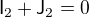 , i.e.
, i.e.
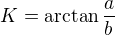 . Then we want to show that
. Then we want to show that
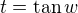 , i.e.
, i.e. 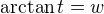 . We get that
. We get that![kopírovat do textarea $
\mathsf I_2+\mathsf J_2&=\int_K^{\frac{\pi}2}\ln(\tan t)\,\mathrm dt+\int_{0}^{\tan K}\frac 1{1+t^2}\ln|t\cdot\cos K-\sin K|\,\mathrm dt\\[.5\baselineskip]
&=\int_K^{\frac{\pi}2}\ln(\tan t)\,\mathrm dt+\int_{0}^{K}\ln|\tan w\cdot\cos K-\sin K|\,\mathrm dw\\[.5\baselineskip]
&=\int_K^{\frac{\pi}2}\ln(\tan t)\,\mathrm dt+\int_{0}^{K}\ln\left|\frac{\sin w}{\cos w}\cdot\cos K-\sin K\right|\mathrm dw\\[.5\baselineskip]
&=\int_K^{\frac{\pi}2}\ln(\tan t)\,\mathrm dt+\int_{0}^{K}\ln\left|\frac{\sin w\cdot\cos K-\sin K\cdot \cos w}{\cos w}\right|\mathrm dw\\[.5\baselineskip]
&=\int_K^{\frac{\pi}2}\ln(\tan t)\,\mathrm dt+\int_{0}^{K}\ln\left|\frac{\sin(w-K)}{\cos w}\right|\mathrm dw\\
[.5\baselineskip]
&=\int_K^{\frac{\pi}2}\ln(\tan t)\,\mathrm dt+\int_{0}^{K}\ln\left|\frac{\sin w}{\cos w}\cdot\frac{\sin(w-K)}{\sin w}\right|\mathrm dw\\[.5\baselineskip]
&=\int_K^{\frac{\pi}2}\ln(\tan t)\,\mathrm dt+\int_{0}^{K}\ln|\tan w|\mathrm dw+\int_{0}^{K}\ln\left|\frac{\sin(w-K)}{\sin w}\right|\mathrm dw\\[.5\baselineskip]
&=\int_K^{\frac{\pi}2}\ln(\tan t)\,\mathrm dt+\int_{0}^{K}\ln(\tan w)\mathrm dw+\int_{0}^{K}\ln\left(\frac{\sin(K-w)}{\sin w}\right)\mathrm dw\\[.5\baselineskip]
&=\underbrace{\int_{0}^{\frac{\pi}2}\ln(\tan w)\mathrm dw}_{\mathsf L_1}+\underbrace{\int_{0}^{K}\ln\left(\frac{\sin(K-w)}{\sin w}\right)\mathrm dw}_{\mathsf L_2}
$](/mathtex/b0/b05d89c5747a973a29b0da8696b728f2.gif)
![kopírovat do textarea $
\mathsf L_1&=\int_{0}^{\frac{\pi}2}\ln(\tan w)\mathrm dw\stackrel{\boldsymbol{\color{red}???}}{=}0\\[.5\baselineskip]
\mathsf L_2&=\int_{0}^{K}\ln\left(\frac{\sin(K-w)}{\sin w}\right)\mathrm dw\stackrel{\boldsymbol{\color{red}???}}{=}0\\[.5\baselineskip]
$](/mathtex/ad/adf5ca2d771e9bdc5da5baebdd4a86ed.gif)
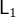 we put a substitution
we put a substitution  and we have that
and we have that![kopírovat do textarea $
\mathsf L_1&=\int_{0}^{\frac{\pi}2}\ln(\tan w)\mathrm dw
=-\int_{\frac{\pi}2}^{0}\ln\left(\tan\left(\frac{\pi}2-z\right)\right)\mathrm dz
=\int_{0}^{\frac{\pi}2}\ln(\cot z)\mathrm dz\\[.5\baselineskip]
&=\int_{0}^{\frac{\pi}2}\ln\left(\frac 1{\tan z}\right)\mathrm dz
=-\int_{0}^{\frac{\pi}2}\ln(\tan z)\mathrm dz
=-\mathsf L_1
$](/mathtex/6f/6fdb942e1fb059270432d4172587d7cc.gif)
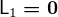
 will be split into two subintegrals. In the former one we will put
will be split into two subintegrals. In the former one we will put  .
.![kopírovat do textarea $
\mathsf L_2&=\int_{0}^{K}\ln\left(\frac{\sin(K-w)}{\sin w}\right)\mathrm dw
=\int_{0}^{K}\ln(\sin(K-w))\mathrm dw-\int_{0}^{K}\ln(\sin w)\mathrm dw\\[.5\baselineskip]
&=-\int_{K}^{0}\ln(\sin(v))\mathrm dv-\int_{0}^{K}\ln(\sin w)\mathrm dw
=\int_{0}^{K}\ln(\sin(v))\mathrm dv-\int_{0}^{K}\ln(\sin w)\mathrm dw\boldsymbol{=0}
$](/mathtex/db/db09d0c17a0d28616b23dbf4d488fa44.gif)
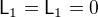 we conclude that
we conclude that 