Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Given det(AB)=4, Then det(BA), where A and B are not square matrix
#1 07. 03. 2016 11:57
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Given det(AB)=4, Then det(BA), where A and B are not square matrix
If 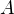 is a matrix of order
is a matrix of order 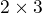 and
and  is a matrix of order
is a matrix of order  and
and  Then
Then 
Offline
#2 07. 03. 2016 12:39
Re: Given det(AB)=4, Then det(BA), where A and B are not square matrix
Hi ↑ stuart clark:,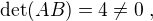 , give
, give  ,
,
so  and
and 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 07. 03. 2016 13:02
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Given det(AB)=4, Then det(BA), where A and B are not square matrix
Thanks ↑ vanok:, would you like to explain me in detail
Offline
#4 08. 03. 2016 00:25
Re: Given det(AB)=4, Then det(BA), where A and B are not square matrix
↑ stuart clark:
Let us define matrices 
Let us assume that  . Using vector notation we have
. Using vector notation we have
If  then the vectors
then the vectors 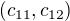 ,
,  would be linearly dependent and
would be linearly dependent and  which is not true.
which is not true.
Considering the fact that  we have
we have  .
.
On the other hand we have
If  then the vectors
then the vectors  ,
,  would be linearly dependent and
would be linearly dependent and  .
.
Therefore  .
.
Next let us define a matrix  such that
such that
Similarly as in the previous cases we have
From the fact that  we deduce that the vectors
we deduce that the vectors  ,
,  ,
, 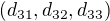 are linearly dependent which implies
are linearly dependent which implies 
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#5 08. 03. 2016 17:04 — Editoval vanok (08. 03. 2016 17:06)
Re: Given det(AB)=4, Then det(BA), where A and B are not square matrix
Hi ↑ stuart clark:,
As regards possible complements for the given solution, there is 2 ways.
The first one is to take advantage your first course of linear algebra (normally made in first year of university); and specially call back it two theorems
The determinant of a matrix M, of type (n, n) is no zero iff his rank  is n.
is n.
And also  A,B matrices of type (m,n),(n,m) resp.
A,B matrices of type (m,n),(n,m) resp.
and simply to apply.
(It is my method).
Other method, (for the high of grammar schools) is the one used by ↑ Pavel: but which is applicable only to this particular situation.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 08. 03. 2016 23:49
Re: Given det(AB)=4, Then det(BA), where A and B are not square matrix
↑ vanok:
The method, I described former, can be used also for matrices of general type  , resp.
, resp.  with
with  not only in this particular case.
not only in this particular case.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#7 09. 03. 2016 08:26
Re: Given det(AB)=4, Then det(BA), where A and B are not square matrix
↑ Pavel:,
A lot of courage for your next exercise with n = 100 and m = 200.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 09. 03. 2016 16:38
Re: Given det(AB)=4, Then det(BA), where A and B are not square matrix
↑ vanok:
Let A be a 100x200 matrix, B be a 200x100 matrix such that det(AB)=4. Prove that det(BA)=0.
Solution:
Let 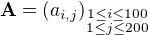 ,
,  ,
,  and
and  . Let us denote
. Let us denote
Then the following identity holds true for 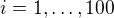 :
:
Among 200 100-dimensional vectors  ,
, 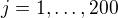 there exist at most 100 vectors
there exist at most 100 vectors 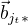 ,
,  that are linearly independent. If
that are linearly independent. If  then all the vectors
then all the vectors  would be linearly dependent and
would be linearly dependent and  . Hence
. Hence 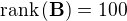 .
.
There is a similar identity for the vectors 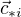 with
with 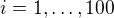 :
:
For the same reasons as in the previous case we can deduce that if  then all the vectors
then all the vectors  would be linearly dependent and
would be linearly dependent and  . Hence
. Hence  .
.
We also have for 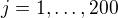

Due to the fact that  we infer that the vectors
we infer that the vectors  ,
, 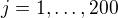 , are linearly dependent.
, are linearly dependent.
Thus
If you wish to examine another case, e.g.  and
and  , I will be glad to show you.
, I will be glad to show you.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#9 09. 03. 2016 16:54
Re: Given det(AB)=4, Then det(BA), where A and B are not square matrix
And it not much costs you to generalize your results and to put you to the same level that I.
Then well continuation.
( I notice that in analysis you used by the very complicated theorems and that in algebra on the contrary you always want to take back, algebraic demonstrations for every result)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 13. 03. 2016 22:12 — Editoval stuart clark (13. 03. 2016 22:14)
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Given det(AB)=4, Then det(BA), where A and B are not square matrix