Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 03. 2016 23:20
- Octavianus

- Příspěvky: 146
- Reputace: 0
Logaritmická rovnice se zlomkem v logaritmu
Ahojte stále se nemůžu dopočítat tohoto příkladu
zadání: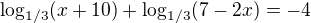
odstraněním logaritmů dostávám: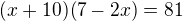
diskriminant vyjde 
kořeny pak -7/2 a -3
to je ale špatně, SPRÁVNÉ výsledky jsou: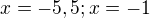
nevíte kde je chyba?
Offline
#3 19. 03. 2016 23:39
- Octavianus

- Příspěvky: 146
- Reputace: 0
Re: Logaritmická rovnice se zlomkem v logaritmu
↑ Elisa:
aha já se přehlédl díky Eliško
Offline


