Matematické Fórum

kolejo · 09. 03. 2016 21:49

Dobrý večer přeji,
našel by se tu nějaký odborník na Gröbnerovy báze? Zápasím tu s jedním příkladem. Už jsem myslel, že jsem tomu přišel na kloub. Chybí mi ale k cíli ještě pár kroků.

Zadání: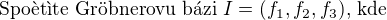
$\text{Spočtěte Gröbnerovu bázi } I=(f_1,f_2,f_3) \text{, kde}$
$f_1=x^2+y+z-1\\ f_2=x+y^2+z-1\\ f_3=x+y+z^2-1.$

Wolfram ukazuje odpověď:
$(x+y+z^2-1,\\ y^2-y-z^2+z,\\ 2yz^2+z^4-z^2,\\ z^6-4z^4+4z^3-z^2)$
...a to vypadá jako dobrá odpověď, chtěl bych k ní dojít sám (tj. umět k ní dojít, proto žádám o pomoc, teď mi připadne, že to sám nedokážu)

Počítám 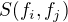$S(f_i,f_j)$ , no díky symetrii je docela jedno, které vezmu, takže: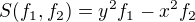
$S(f_1,f_2) = y^2f_1-x^2f_2$
To podle vedoucích koeficientů, tímto se jich zbavím. Pak je potřeba dále se zbavovat koeficientů a postupně jsem došel (nebudu to sem dávat celé) k následující kombinaci: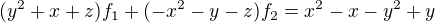
$(y^2+x+z)f_1+(-x^2-y-z)f_2=x^2-x-y^2+y$
Symetricky se lze dostat k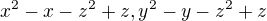
$x^2-x-z^2+z,y^2-y-z^2+z$ .

Teď nevím, jestli vzít dva z nich a na konci se jednoho zbavím, nebo už teď mi stačí přidat ten wolframem napovězený třetí. Řekněme, že pojedu takto: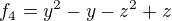
$f_4=y^2-y-z^2+z$

a potřebuji dále počítat 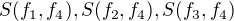$S(f_1,f_4),S(f_2,f_4),S(f_3,f_4)$

Ono se s tím počítá jako s kongruencemi, mám: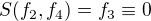
$S(f_2,f_4)=f_3\equiv 0$
$S(f_3,f_4)=f_2\equiv 0$

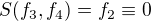
A s 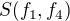$S(f_1,f_4)$ mám pořád problém, možná nakonec mám vzít 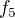$f_5$ nějaký ten symetrický a počítat $S(f_4,f_5)$ ?

$S(f_1,f_4)=y^2f_1-x^2f_4=\\ =x^2y+x^2z^2-x^2z+y^3+y^2z-y^2$

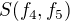Jak s tímhle pak pracovat? Můžu x^2 nahradit 1-y-z (protože f_1), a y+z^2-z nahradit y^2 (protože f_4)...
$x^2y+x^2z^2-x^2z+y^3+y^2z-y^2=\\ =x^2(y+z^2-z)+y^2(y+z-1)=\\ =(1-y-z)y^2+y^2(y+z-1)$

To je nula? Je to dobře? Jak mám pokračovat v tomto Buchbergerově algoritmu?
Děkuji za jakoukoliv radu.
kolejo

kolejo · 20. 03. 2016 10:49

↑ kolejo:

nazdar kolejo, ty měchu, už jsem na to přišel. je to fakt jednoduchý, tys na to šel totiž docela blbě! (špatně jsi pochopil to uspořádání)
nebudu ti to TeXovat, to je zbytečný, se v tom vyznáš, ne?

nejdřív vezmeš S(f2,f3)=f2-f3=y^2-y-z^z+z, to je tvůj f4 a máš ho hned.
S(f1,f3)=f1-xf3=-xy-xz^2+x+y^2+yz^2+z-1
přičti yf3 ... -xz^2+x+y^2+yz^2+z-1
přičti z^2f3 ... x+y^2+2yz^2+z^4-z^2+z-1
přičti -f2 (to jest odečti f2, f2=f3+f4 btw)
f4=2yz^2+z^4-z^2
S(f4,f5)=2z^2f4+(-y+z^2*1/2+1/2)f5
to je jako celá kombinace, pak vyhodíš f1,f2, a máš čtyři polynomy v bázi...
není to všechno, ale takhle ti to stačí, žejo?
když tak dej vědět. jsem na příjmu

kolejo · 20. 03. 2016 10:50

↑ kolejo:

Jó, díky, už tomu rozumím. Takhle mi to stačí.
Měj se, a označuji za vyřešené.

Matematické Fórum

#1 09. 03. 2016 21:49

Gröbnerova báze

#2 20. 03. 2016 10:49

Re: Gröbnerova báze

#3 20. 03. 2016 10:50

Re: Gröbnerova báze

Zápatí